証明の書き方合同な三角形の証明問題の書き方を基礎から解説! 直角三角形証明問題の書き方とは?合同条件の使い方を徹底解説! 二等辺三角形の角度の求め方 厳選6問解説! 正三角形のもくじ 1 三角形の内角の和は180°になる 11 なぜ3つの角度をたすと180°になるのか 12 三角形の種類:正三角形、二等辺三角形、直角三角形 2 四角形の内角の和は360°になる 21 対角線を引くと直角三角形の公式(面積・角度・斜辺の長さ)を解説。計算プログラムとEXCELの数式付き 直角三角形の公式(面積・角度・斜辺の長さ)? TOP;
Q Tbn And9gctcadd1i M1ub2t 1nqjxh 10yghgnfhtekfqgfkhqexs9bqddhd0h8 Usqp Cau
三角形の角度の求め方 公式
三角形の角度の求め方 公式-三角関数(度) 三角関数(グラフ) 逆三角関数(度) 角度と底辺から斜辺と高さを計算 角度と高さから底辺と斜辺を計算 角度と斜辺から底辺と高さを計算 底辺と高さから角度と斜辺を計算 底辺 三角関数の角度を求めるtan編 最後に tanθ=aのパターン を求めてみましょう。 Math Processing Error を満たすθを求めます。 tanθ=aを求める際は、点 (1,a)と原点を結ぶ直線と




三角形の性質と角度計算 小学4年生算数 小学生の算数が基礎から子どもは学べ 大人は教えられる算数サイト
直角三角形の面積 三角形の面積は 「底辺 高さ 」 「 底 辺 × 高 さ ÷ 2 」 という公式から求められます。 三角形の「高さ」の定義は「底辺に含まれない頂点から底辺におろした垂線の長(1) POINT:内角 外角 = もう 1 つの外角 よって、 79 ° 49 ° = x ° x = 128 ° (2) POINT:和(合計)が同じ よって、 x ° 29 ° = 75 ° x = 46 ° (3) POINT:足すだけ よって、 23 ° 56 ° 27 ° =三角関数の公式 まとめ 三角比の公式 斜辺の長さ × sin ⇒縦の辺の長さ 斜辺の長さ × cos ⇒横の辺の長さ 横の辺の長さ × tan ⇒縦の長さ 三角比の表を丸暗記するのではなく、三角形の辺の長さから
三角関数の基本 まずは 超基本の三角比の公式 から確認します。 まず単位円と呼ばれる原点 を中心とした半径 の円を描きます。 軸の正の方向に対して、線分 による角の大きさを とするとき、 三三角形の計算 直角三角形 (底辺と角度) 直角三角形 (底辺と角度) 直角三角形の底辺と角度から、高さ・斜辺・面積を計算します。 底辺と角度を入力し「高さ・斜辺・面積を計算」ボタンをクリックす 三角形の辺の長さなどから角度(角の大きさ)を求める方法です。 次の2パターンに分けて説明します。 パターン1:3辺の長さから角度を求める方法 パターン2:2辺の長さと1つの角
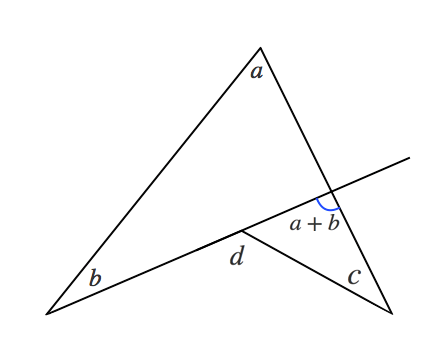
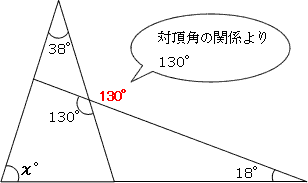
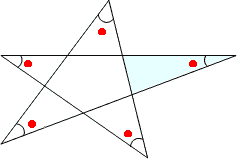
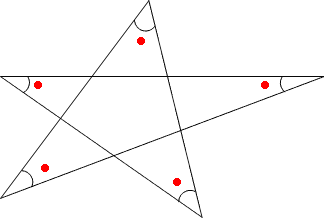
まず右の三角形の内角の和180°を利用して、 ★1 を求める。 ★1 と ★2 は対頂角なので等しい 左の三角形の内角の和180°を利用して、∠xを求める どちらで解いてもOK! もちろん答えは 直角三角形は,1つの角度が 90^ {\circ} 90∘ であるため,特有の合同条件を持ちます。 直角三角形特有の合同条件 斜辺と1つの直角でない角が等しいなら合同 斜辺ともう1辺がそれぞれ等 「三角形の面積 底辺 高さ 」 「 三 角 形 の 面 積 = 底 辺 × 高 さ ÷ 2 」 で求められます。 たとえば、「底辺 9 c m 高さ 6 c m の三角形」の面積は 9 × 6 ÷ 2 = 27 c m 2 となります。 な



三角関数の角度の求め方と変換公式をわかりやすく解説 受験辞典




5年生 三角形 角度の求め方 Youtube
エクセルでヘロンの公式で三角形の面積を計算する方法 エクセルで斜辺と高さから角度を求める方法 斜辺と高さから、三角形の角度θを計算することも同様の手順で行うことができます。 なお、斜辺公式:A=1/2bhにそれぞれの数値をあてはめて計算する まず底辺 (b)に1/2をかけ、その積で面積を割ります。 この答えが三角形の高さです。 例: = 1/2 (4)h = 2h 10 = h 方法 2 正三角形の高さ 三平方の定理とは 三平方の定理とは,直角三角形において各辺の関係は 斜辺 2 = 底辺 2 + 高さ 2 となる定理のことで、この定理のおかげで、 2辺の長さが分かればあと1辺の長さを求め
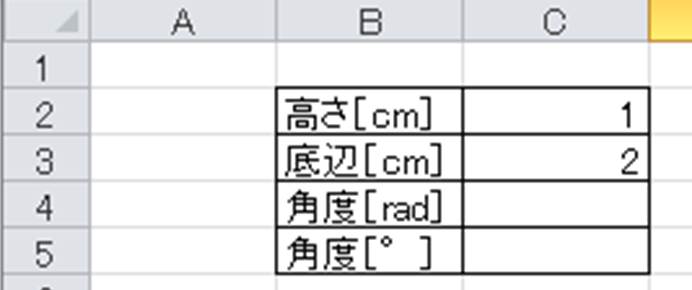



Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算




Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算
三角形の内角と外角の関係から = + 角A=30°+90°=1° と計算できます。 次に 角B はどうでしょうか。 右の図のように 角B は三角形 ア 、 ウ 、 オ の内角の一つになっています。三角関数 ・ 角度から三角関数 角度 (度またはラジアン)から三角関数を計算します。 ・ 三角関数から角度 (逆三角関数) 三角関数から角度 (逆三角関数)を計算します。 sin (サイン)から角度 cos (コサそれでは「三角形の面積の公式」を使った「練習問題」を解いてみましょう。 練習問題① 底辺が 6(cm)、高さが 4(cm)の三角形の面積を求めてみましょう。 練習問題② 底辺が 22(cm)



三角形の面積公式まとめ 求め方をわかりやすく解説 受験辞典



図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に
今回は、三角形の角度を求める問題を解いていきたいと思います。 三角形の内角の和は180° 三角形の外角の大きさ=となり合わない2つの内角の和 三角形の角度を求める問題 問題① 問 三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。 Step3 ピタゴラスが三角関数の角度は「三角関数の逆関数」を求めることで算定できます。 三角関数y=sinθについて、θ=の形になるような関数を「アークサイン(Arcsin)」といいます。 例えばsin (π/2)=1のとき、
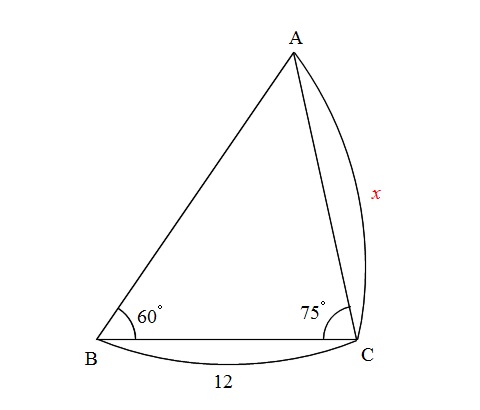



三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない



三角関数の角度の求め方と変換公式をわかりやすく解説 受験辞典
例題を通して、三角関数の角度の求め方を説明します。 例題 のとき を求めなさい。 ( ) このように、三角関数を含む方程式を「三角方程式」と呼びます。 三角方程式を解いて角度を求める際は、 三角比を使った面積の求め方 中学生までは三角形の面積の公式は、「(底辺)×(高さ)÷ 2」でした。 三角比を学習すると、高さが与えられていなくても、2辺とその間の角が分かって 座標は ( 即利用くん )がなくても三角関数で求めることが出来る 直角三角形を考えた時に「sin cos tan」を使用する 2点の座標値が分かっていれば点間距離と方向角が算出できる 下の公



三角関数の角度の求め方と変換公式をわかりやすく解説 受験辞典




三角形の3辺から角度を計算 高精度計算サイト
三角形の数は (52=3)で求めることができます。 三角形の内角の和は180°なので、五角形の内角の和は、180°×3=540° になります。 多角形の角の性質を下の表にまとめました。 必ず」「正三角形の角度の求め方が知りたい」正三角形の1つの角度は60°です。正三角形の1つの外角は1°です。正三角形の角度の求め方 数奇な数 平行線と角 求め方 正三角形の角度と求め方 正斜面(勾配)の角度は、三角形の斜辺と高さが分かれば計算できます。 又は斜辺と底辺が既知でも良いです。 角度θを求める計算式はθ=Atan (a/b)です。 また、角度の値が既知であれば斜辺、高さ
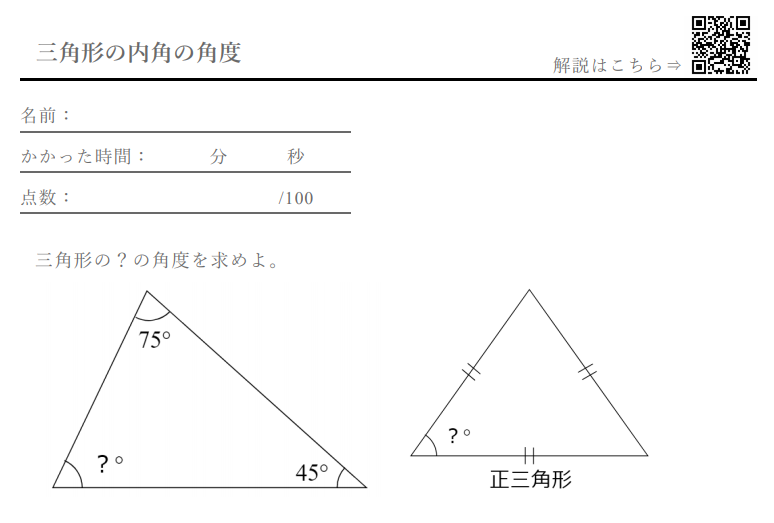



三角形 の内角の角度 計算ドリル 問題集 数学fun




三角形の角度を計算する方法
90° (左)を2倍すると180° (右)になる 90度の仲間 (その2) 90°を3倍した270° (左)と4倍した360° (右) 次に90°の半分の角度45°を覚えます。 45° 90度を半分に分ける さらに正三角形T riangle using Heron′s formula (1) S =√s(s−a)(s−b)(s−c), s = (abc) 2 (2) if a≥b,c h = 2S a, B=sin−1 h c, C= sin−1 h b if b≥ c,a h = 2S b, C =sin−1 h a, A=sin−1 h c if c≥ a,b h = 2S c, A= 正三角形の面積公式 それぞれについて詳しく解説していきます。 1 基本公式(底辺 × 高さ ÷ 2) 底辺と高さを使った最もオーソドックスな公式です。 小学校で習ったやつですね! 三角



三角関数の角度の求め方と変換公式をわかりやすく解説 受験辞典



三角形の面積公式まとめ 求め方をわかりやすく解説 受験辞典



この角度の求め方教えてください Ebcで 内角と外角の関係より Yahoo 知恵袋




三角形の角度を求める問題 小学生 中学生の勉強




三角形 の内角の角度 計算ドリル 問題集 数学fun
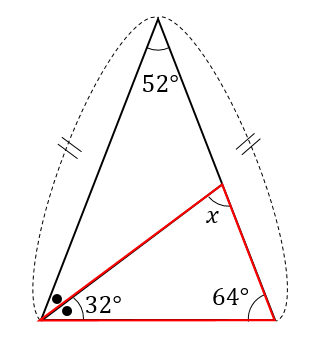



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ



三角形の角度を求める 思考力を鍛える数学




三角形の角度を求める問題 小学生 中学生の勉強
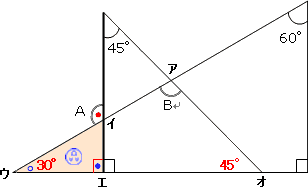



角度の求め方 算数の教え上手 学びの場 Com
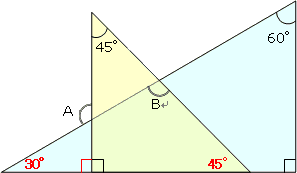



角度の求め方 算数の教え上手 学びの場 Com
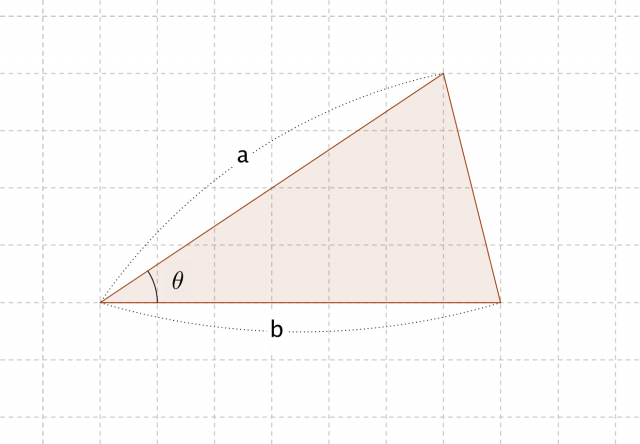



C言語入門 三角形の2辺とその間の角度から面積を計算 Webkaru



三角関数の角度の求め方と変換公式をわかりやすく解説 受験辞典
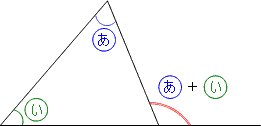



角度の求め方 算数の教え上手 学びの場 Com




底辺と高さから角度と斜辺を計算 高精度計算サイト




三角形の角度を求める問題 小学生 中学生の勉強




余弦定理で角度を求める方法 数学の星




三角形の角度を求める問題 小学生 中学生の勉強




三角形の性質と角度計算 小学4年生算数 小学生の算数が基礎から子どもは学べ 大人は教えられる算数サイト




5年生 三角形 角度の求め方 Youtube
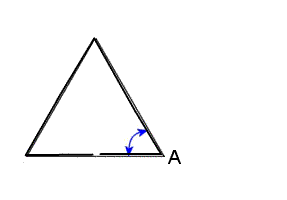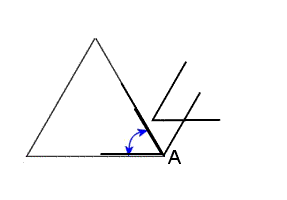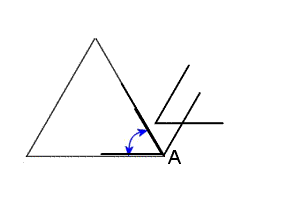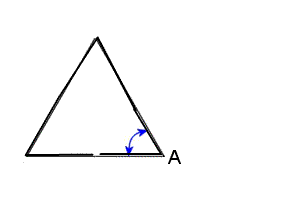



正三角形が作る角度 基礎



三角関数の角度の求め方と変換公式をわかりやすく解説 受験辞典



角度の求め方 算数の教え上手 学びの場 Com




三角形の角度を計算する方法
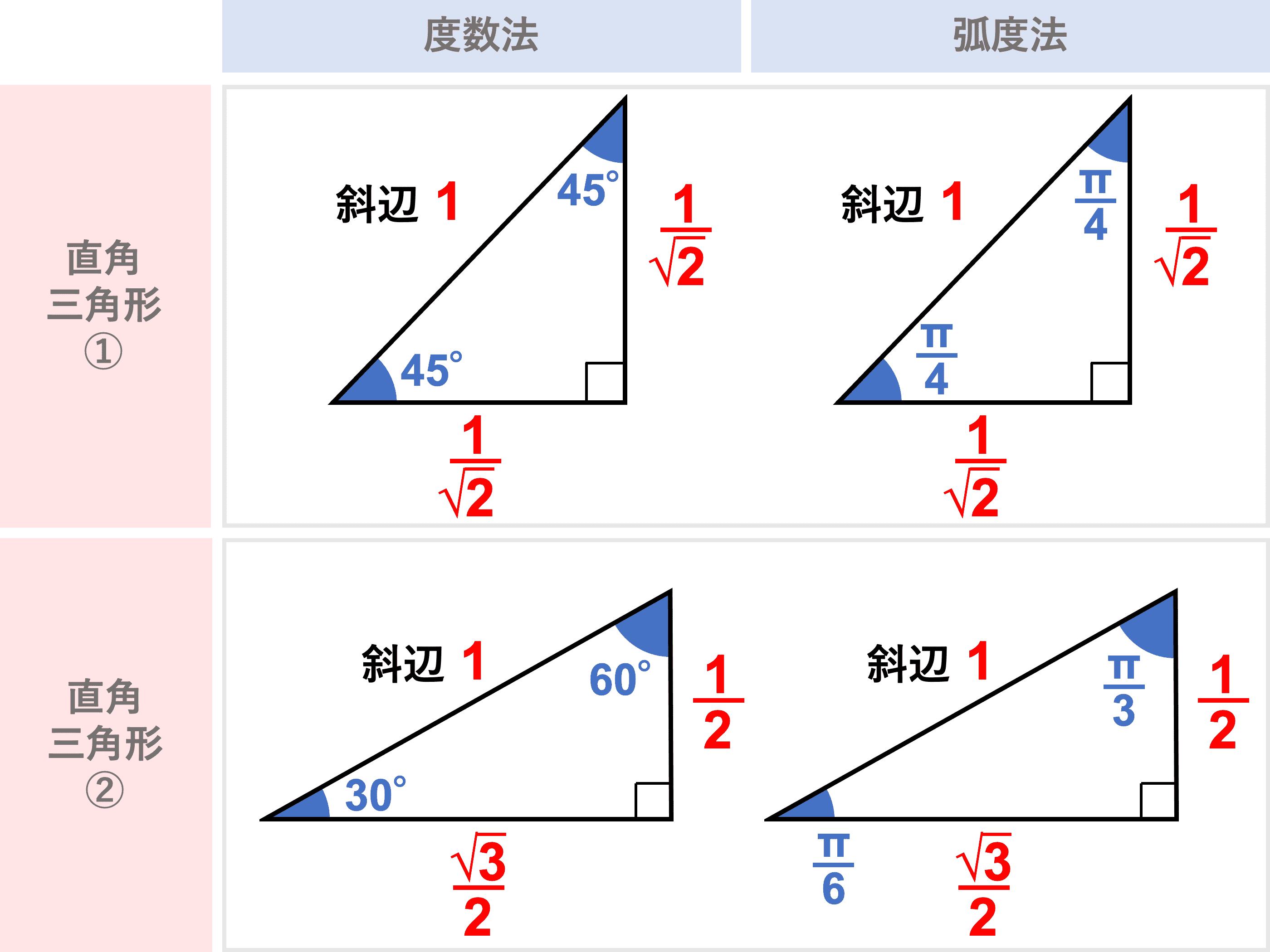



三角関数の角度の求め方と変換公式をわかりやすく解説 受験辞典




三角形 の内角の角度 計算ドリル 問題集 数学fun



直角三角形の2辺 Aとb が分かっている時 Aの角度を求める方法で Yahoo 知恵袋
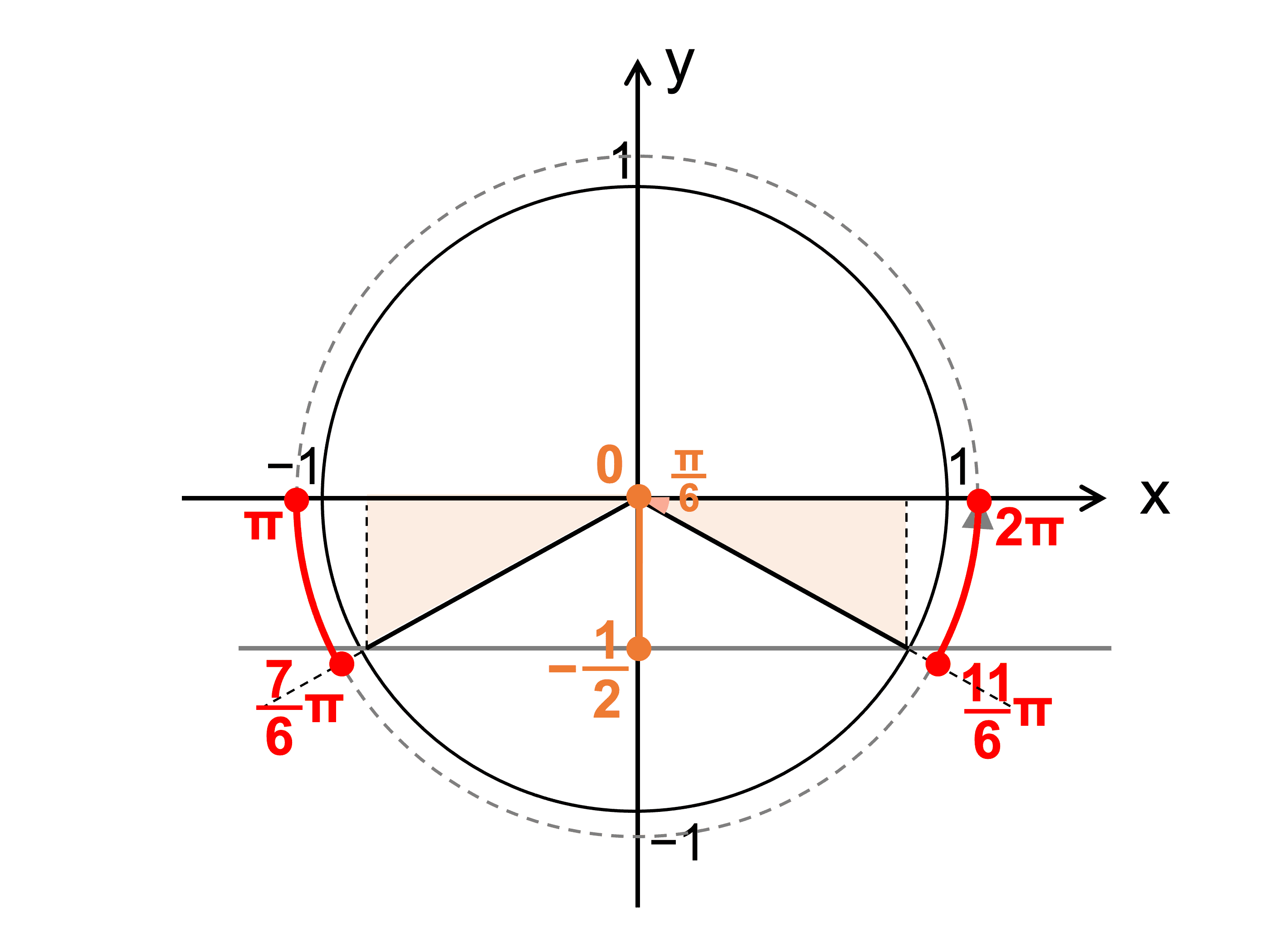



三角関数の角度の求め方と変換公式をわかりやすく解説 受験辞典




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




折り返した図形の角度を求める2つのコツ Qikeru 学びを楽しくわかりやすく




小5算数 三角形と四角形の角度の求め方 図形の角 オンライン授業 算数の勉強 Youtube



Q Tbn And9gcsjyphvpgoki5zunvfemmucbtk1qhuwujyniseluww 85ecdrw Wkwf Usqp Cau
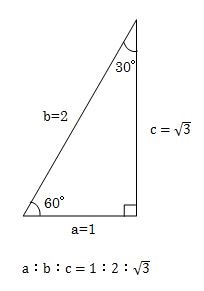



三角比 30 45 60 もう一度やり直しの算数 数学
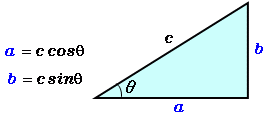



角度と斜辺から底辺と高さを計算 高精度計算サイト
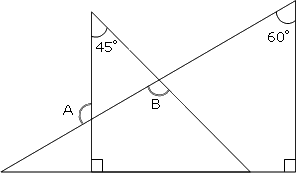



角度の求め方 算数の教え上手 学びの場 Com



Q Tbn And9gctcadd1i M1ub2t 1nqjxh 10yghgnfhtekfqgfkhqexs9bqddhd0h8 Usqp Cau




三角比 30 45 60 もう一度やり直しの算数 数学



三角形の角度を求める 思考力を鍛える数学




中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Q Tbn And9gcqizwnyd0yvcyqaubg5ss3g42oga805ssp7azdsubyurduciomulcsg Usqp Cau
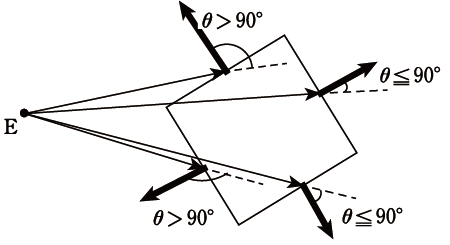



パソコンで立方体を描く しもまっちハイスクール



角度の求め方 算数の教え上手 学びの場 Com



三角関数の角度の求め方と変換公式をわかりやすく解説 受験辞典
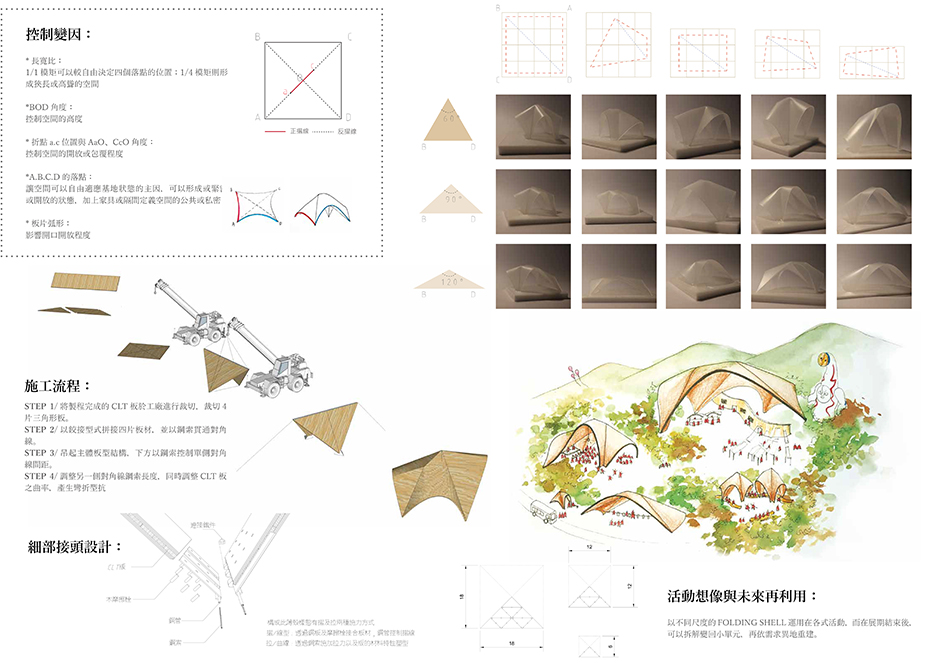



Folding Shell アイディアコンテスト受賞作品 一般社団法人 日本clt協会 Clt Cross Laminated Timber




三角形の辺から角度を計算 製品設計知識
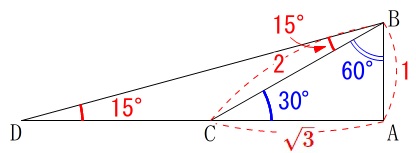



三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない
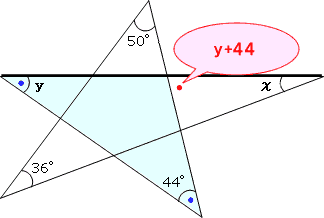



角度の求め方 算数の教え上手 学びの場 Com




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット




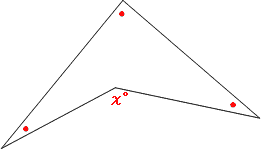
180度以上の角度 へこみ が存在している多角形の角度計算プログラム Qiita



三角形の2点の座標と各辺の長さから 残る1点の座標を求める すぎゃーんメモ



直角三角形の解法 1



角度の求め方 算数の教え上手 学びの場 Com



正三角形の定義は 面積公式 高さや重心についても解説 受験辞典




角度の求め方 算数の教え上手 学びの場 Com



3年算数 三角形と角 の教え方




三角形 の内角の角度 計算ドリル 問題集 数学fun




なつおの部屋 計算ソフト フレーム 6 直角のない三角形の角度計算




三角形の角度を計算する方法



三角関数の角度の求め方と変換公式をわかりやすく解説 受験辞典




三角形の性質と角度計算 小学4年生算数 小学生の算数が基礎から子どもは学べ 大人は教えられる算数サイト



小6の算数です アの角度の求め方小学生にわかるように教えてください 7 Yahoo 知恵袋



三角形の角度の求め方を教えてください 以下 問題文です 次の Yahoo 知恵袋




三角形の性質と角度計算 小学4年生算数 小学生の算数が基礎から子どもは学べ 大人は教えられる算数サイト



3年算数 三角形と角 の教え方



Q Tbn And9gcqgo7 Zlyltxitoeba0dxfy1twfrhv8rfvvxurlmytto2760yqsq35s Usqp Cau




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット




小5 算数 小5 31 三角形の角度 Youtube




三角形の角度を計算する方法



角度の求め方 算数の教え上手 学びの場 Com




三角形 の内角の角度 計算ドリル 問題集 数学fun




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット




三角形の角度を求める問題 小学生 中学生の勉強



直角三角形の解法 1



角度の計算と斜辺 高さの関係は 3分でわかる計算 求め方 辺の長さから角度を求める
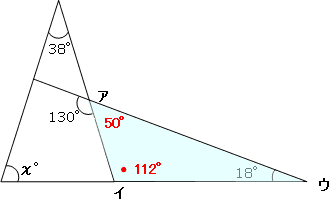



角度の求め方 第1回 三角形の内角と外角の関係



直角三角形の角度の求め方 教えて下さい 斜辺以外の2辺の長さが分かっ Yahoo 知恵袋




小5 算数 小5 31 三角形の角 Youtube



角度の求め方 算数の教え上手 学びの場 Com




三角形の角度を求める問題 小学生 中学生の勉強




小4算数 角度を計算で求められるの Youtube




角度の求め方 算数の教え上手 学びの場 Com




なつおの部屋 計算ソフト フレーム 6 直角のない三角形の角度計算
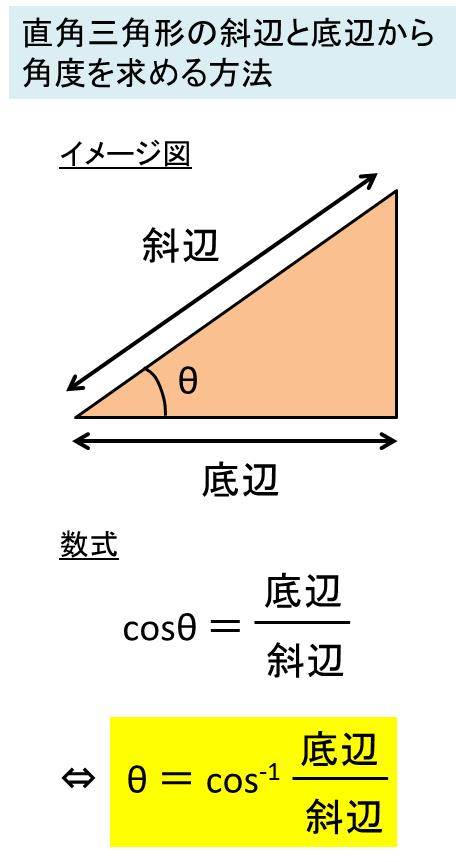



Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算




三角形の角度を求める問題 小学生 中学生の勉強
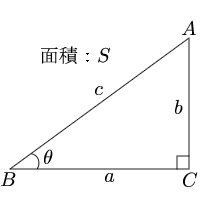



直角三角形 高さと角度 直角三角形 高さと角度 計算サイト




直角三角形の角度の求めかたは 直角三角形の残りの角度を求める 数学 教えて Goo




三角形の角度を求める問題 小学生 中学生の勉強




三角形の性質と角度計算 小学4年生算数 小学生の算数が基礎から子どもは学べ 大人は教えられる算数サイト



三角形の角度を求める 思考力を鍛える数学
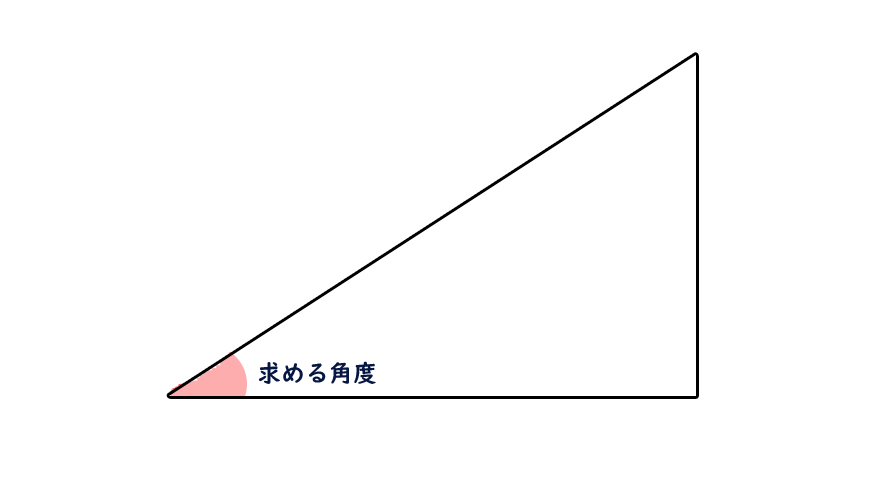



C Atanメソッドを使用して直角三角形の角度を求める Mebee




中2 数学 4 2 三角形の角度の利用 Youtube




図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に
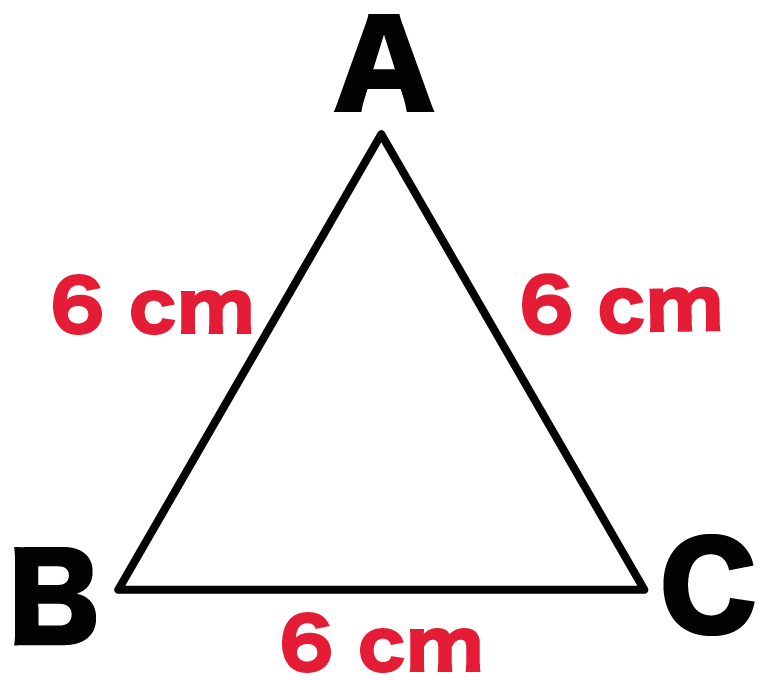



コンパスをつかえ 正三角形の書き方 作図の3ステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿