++ 50 ++ 連立 方程式 の やり方 192845-連立方程式のやり方

 連立方程式を 代入法で解く方法 について解説していくよ！ 連立方程式を解くためには 『加減法』と『代入法』という2つの解き方があったよね。連立方程式とは？ 連立方程式の加減法1（2式をたす・ひく） 連立方程式の加減法2（係数をそろえる） 連立法的式の代入法 今回は、2つの方程式を組みにした「連立方程式」を学習します 中2数学で一番大切と言っても良い単元ですので、一緒にしっかりやっていきましょう ホーム;

連立方程式の加減法 大人の学び直し算数 計算のやり方解説 無料

連立方程式のやり方

連立方程式のやり方-連立方程式の解き方 2つの式から x や y の値を求めることを 連立方程式 （れんりつほうていしき）と言います。例えば、連立方程式を文章問題にすると以下 連立方程式の解き方をみわける2つのコツ 連立方程式の解き方（加減法or代入法）を見分けるコツは、 代入法で解く特殊なケースを覚える ってことさ。 これを覚えちゃえば、 特殊なケースに出くわしたら「代入法」、 ソレ以外は「加減法」で解けるよね

第１章 連立方程式

 解き方 numpylinalgsolve を使って次のように計算できる。 結果は次のとおりとなる。 array ( 1, 2, 3 ) 1組の 連立方程式 を単発で解く場合は上の方法で問題ないが、 A の部分は変わらずに b が変わる場合を数多く解く場合には次のLU分解を使うやり方のほう中2の数学（連立方程式）です！ やり方と答えが分からないので分かる方、解説お願いします🙇🏻‍♀️🙏🏻 9」家から2km離れた駅に行った。はじめは 全速0mで歩き、途中から分きっ40mで 2 きったり、馬駅につくまでに1円分ラウた。 歩いた道のりを、 走った着のりを求めな土い。 ある中 問題文に出てくる2つをそれぞれx、yに置き換え、連立方程式にする解き方が一般的です。 ここでは基本問題を挙げつつ、それ以外のSPIなどで時短として紹介される解き方の方法を簡単に説明していきます。 目次 1 非・連立方程式のつるかめ算 2 つると

先日連立方程式の解き方のコツ で、連立方程式は加減法、代入法があり、どちらのやり方でも解ける。 学校でもこの2つのやり方を勉強します。 そして、まずは加減法をしっかり学習しましょうとお話 ここでは、そんな比例式を含んだ連立方程式の解き方を解説します。 ※比例式とは？ 比例式とは、「ab = xy」や「abc = xyz」「ab = xy = mn」のように、 「複数の比が等しいことを表した式」のことです。 比例式が出てきた場合、そのままの形だと使いにくいので、方程式に直しましょう。 「ab = xy」 (ただしa, b, x, y はすべて0でない) という比例式は連立方程式とは2つの文字(xとy)を含み、2つの式からなる方程式のこと。 連立方程式の解き方には 代入法 と 加減法 がある。 どちらの場合もxかyのどちらか 1つの文字を消去して解く 。 代入法 ≫ 加減法 片方の式が x = の形になっていれば、それを他方のxに代入することでxが消えてyだけの方程式ができる。 (y= の形ならyに代入する。

 連立方程式は掃出法と言われるやり方で機械的に解くことができます。 まず、4つの式のうちaの係数の絶対値がが最も小さいものを選びます。複数ある場合はどれでもいいです 今回ならば①式です 次に、その①式を何倍かして残りの3つの式のaを消去します 次に、いまaを消した式に対してbの ちょっと弟が連立方程式のやり方が分からないというので問題を見てたんですが、私も忘れてます、、、。で、問題なのですが、｛ 3x 2y ＝ 8 5x 3y ＝7という問題なのですが、すみませんがやり方を教えてくれるとありがた 行基本変形のやり方や掛け算での表し方を簡単に解説！ 連立方程式 線形代数連立方程式の解き方を徹底解説！ 連立方程式 掃き出し法のやり方を分かりやすく解説！ サイト内検索 検索 書いてる人 こんにちは！このサイトを運営している現役理系大学生の「く

中2 数学 連立方程式の解き方二通りを解説 授業動画あり アオイのホームルーム

うさぎでもわかる微分方程式 Part11 対角化を用いた連立微分方程式の解き方と指数行列 工業大学生ももやまのうさぎ塾

 これで連立方程式を次のように書きかえることができます。あとは計算あるのみです。 あとは計算あるのみです。 $$①\begin{eqnarray} \left\{ \begin{array}{l} 02x03y =02 \\ 5x2y=17 \end{array} \right \end{eqnarray}$$1つの方程式の両辺を何倍かしただけでは係数がそろわないときは、それぞれ何倍かしてそろうようにします。 これは分数の通分と同じ考え方です。 この問題では (1)を4倍する と −12y ができ、 (2)を3倍する と 12y ができるので、足し算により y が消去できて x だけの方程式になります。 → (3) (3)の結果を (1)か (2)のどちらかに代入すると、もう一つの未知数も求まり 当ページでは、掃き出し方を使って連立1次方程式の解を求める方法や実際に連立1次方程式の解を求める手順を各ステップごとに丁寧に解説しています。 クラメルの公式で解く方法に関してはこちらで紹介しております。 掃き出し法を用いた連立1次方程式の解法 掃き出し法を用いた連立1次

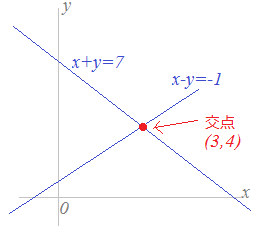
連立方程式とグラフ

連立方程式の解き方 移項と展開 Youtube

連立方程式の解き方 連立方程式の解き方は、下記の2つがあります。 加減法 ⇒ 1つの未知数が消えるように2つの方程式を加減し、もう一方の未知数の解を求める方法 代入法 ⇒ 1つの式を「x=」の形にして、もう一方の式に代入し解を求める方法 本当なら 2 x – 2 y = 4 2 x – 2 y = 4 になっていなければなりません。 { x – y = 2 2 x – 2 y = 3 { x – y = 2 2 x – 2 y = 3 この連立方程式を行列を用いて解いてみましょう。 すると、このように2行目の左側が全て0になってしまいました。 つまり 0 = − 1 0 = − 1 という 明らかに矛盾している式 が出来てしまうのです。 こんな感じに、元の連立方程式に矛盾が含まれ中2数学 中2数学「連立方程式の計算」の問題 どこよりも簡単な解き方・求め方 kazunokazu 21

U9j580gf8iba369ji2w Xyz P 703

連立方程式の解き方と交点の座標の求め方 数学の偏差値を上げて合格を目指す

つまり、連立方程式は鶴亀算の一般化であると同時に、加減法の意味は左のように説明できるということを示している。 このことは、連立方程式の側から言うと、式に具体的な意味を持たせることができるということであり、鶴亀算の側から言えば、この方法も十分にアルゴリズム化ができるということを示している。 例えば、 ・係数をそろえる＝どちらかの足2つの未知数 x, y のどちらかの 係数が等しいとき は、左辺どうし、右辺どうしをそれぞれ 引く と1文字を消去できます。 この問題では y の係数がそろっているので、 y が消去できて x だけの方程式になります。 →(3) (3)の結果を(1)か(2)のどちらかに代入すると、もう一つの未知数も求まります。作成者：黒田匡迪, 辻栄周平（監修：数学教室） 31 はじめに 「vol 1 行列の基本変形のやり方」において, 以下の3つの問題 問題1 連立一次方程式を解く問題 問題2 逆行列を求める問題 問題3 行列式を求める問題 は基本変形を繰り返し行うことで, 解くことが出来ると述べました

1

連立方程式の加減法 大人の学び直し算数 計算のやり方解説 無料

連立方程式を解く 連立方程式を解くには,xかyのどちらかの文字を1つ消去して,文字が1つだけの方程式にして解く。 この解き方に加減法と代入法がある。 加減法 x,またはyの係数をそろえて2つの式を 「たす」または「ひく」して文字を一つ消す。 先ほども言いましたが、連立方程式は 「文字を1つずつ消去していく」 のがオーソドックスなやり方です。 文字を1つ消すためには、式は2つ必要です。 これは、式が2つの連立方程式においていつもやっていることですよね？ 1 連立方程式の加減法を使った解き方 11 手順①\(x\)または\(y\)の係数を揃える 12 手順②係数が同じ符号ならそれぞれの式を引く、異なる符号なら足す。

中2数学 カッコ 分数を含む連立方程式 例題編 映像授業のtry It トライイット

高校数学で学習する連立方程式の解き方まとめ 数スタ

 連立不等式の解き方：二次不等式編 次は二次不等式です。基本的なやり方は一次不等式と変わらないので例題で確認しましょう。 二次不等式の問題 連立方程式 \begin{eqnarray} \left\{ \begin{array}{l} 2x^25x3連立方程式 を解け． （東京都15年） 解説を見る とも係数がそろっていない． の係数をそろえるには， (1)式を5倍， (2)式を9倍するとよい． ※こんな分数の答えになってしまったら，合っているかどうか心配になるが，検算して成り立っていれば3つの文字、式の連立方程式を解くためには まず、文字を1つ消してやることがポイントでしたね！ そうすることで今まで解いてきた連立方程式と同じ形を作ることができます。 たくさん練習して、しっかりと手順を身につけておこうね(^^)

連立方程式の解き方 係数に分数がふくまれる場合 Youtube

中学数学 連立方程式 の効果的な教え方 導入と指導上の注意点

動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru 連立方程式の加減法 このレッスンでは連立方程式の加減法を使った解き方を学びます。 加減法は揃えて消すというものです、揃えて式を整えていきましょう。 スライドはスマホで見る場合スライドしていただくこともできますし、キーボードの左右のボタンを利用していただくこともで二つのやり方で，同じ解になることを確認しなさい。 両方を何倍かして加減する （5） − =− − = 4 3 3 23 x y x y （6） = − = 3 2 4 4 5 13 x y x y 同じ答えが出ることを確認し，解法の比較をしましょう。 連立方程式③ 連立方程式の解き方(1)C 学 年 年 年 組 氏名 学習日： 月 日（ ） 中学校

1

連立方程式 分数と整数が混じった計算の解き方をイチから解説 中学数学 理科の学習まとめサイト

復習連立方程式の解き方 連立方程式とは、一般的に \begin{eqnarray}\left\{\begin{array}{l}axby=c\\dxey=f\end{array}\right\end{eqnarray} といった形で表すことが多い式です。 2元1次方程式と呼ばれる「2つの変数(文字)」と「最大次数が1」の式で表されます。 連立方程式の解き方は大きく2つあります。それは、連立方程式とは問題に書いていませんが、1次関数でも連立方程式は必要になります。 計算でつまずく人は少ないですが、「交点」とあれば「連立」、これは忘れないでくださいね。 ⇒ 加減法とは？連立方程式の解き方とポイント 連立方程式の解き方の鉄板である「消去法」をおさらいした上で、それを行列で考えます。 サイト内検索 あらゆるワードの関連記事を検索できます！ おぐえもん 情報系大学院の出身です♪Webサイトやチラシ、冊子などのデザインや、システム開発などの経験があります。音楽が好きで

連立方程式の問題 高校の範囲でも登場する大切な分野だ 中学や高校の数学の計算問題

中２ 連立方程式の解き方 文字消去でレベルダウン 教えたい 人のための 数学講座

連立方程式 A B Cの3つ式があるときの解き方を解説 中学数学 理科の学習まとめサイト

Studydoctor三元連立方程式 ２ 中２数学 Studydoctor

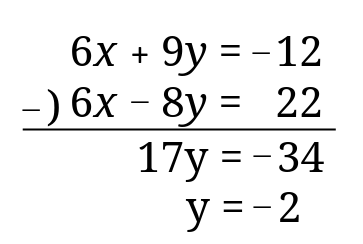
連立方程式を見直ししてもうっかりケアレスミスをしてしまうときの対処法 さびねこ中学校

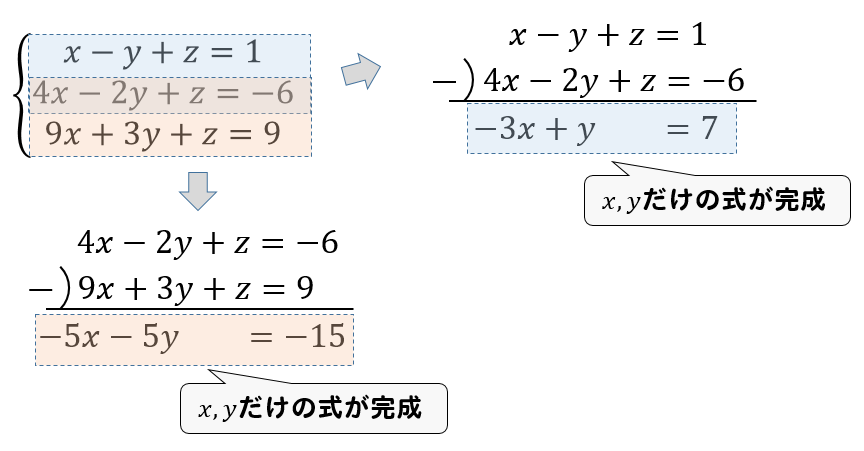
連立方程式３つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト

小数の連立方程式の解き方 両辺を１０倍や１００倍しよう 中学や高校の数学の計算問題

Studydoctor連立方程式の解き方 加減法 中２数学 Studydoctor

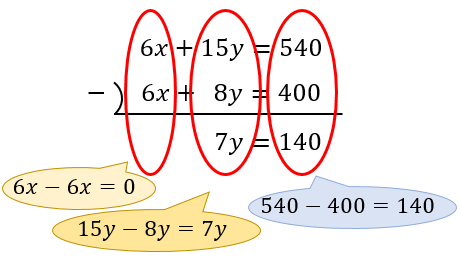
連立方程式 加減法 の解き方 なぜ加減法が成り立つか アタリマエ

こんな風に なぜ連立方程式で交点がわかるんですか Clear

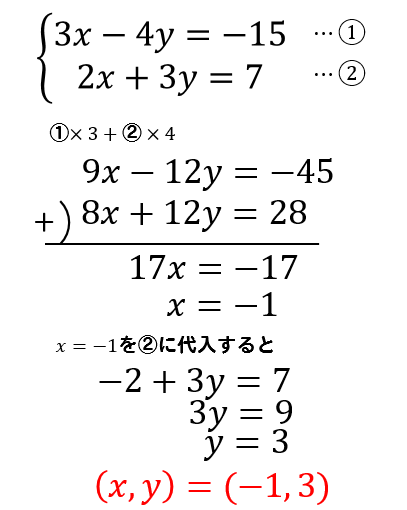
連立方程式 加減法の解き方をわかりやすく問題を使って徹底解説 数スタ

中学数学 連立方程式 代入法 中学数学の無料オンライン学習サイトchu Su

5 1 連立方程式 基本 勉強できようサイト

連立方程式 連立方程式の加減法と代入法 中学数学 定期テスト対策サイト

中2数学 連立方程式の解き方と定期テスト予想問題 Pikuu

連立方程式で３つの式がある時の解き方が誰でも分かる 高校生向け受験応援メディア 受験のミカタ

第１章 連立方程式

お勉強 連立方程式の解き方のご提案 去年の男子女子ｘ ｙ人の問題 そらの暇つぶしch

連立方程式の代入法 簡単な問題で やり方をわかりやすく紹介 中学や高校の数学の計算問題

1

中学数学 中学２年 Vol 0 連立方程式の解き方 代入法 Youtube

数学の連立方程式のやり方が分かりません 教えてくれると有難いです Clear

連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学

連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点

中2数学 連立方程式の文章題 割合 練習編 映像授業のtry It トライイット

連立方程式 1 代入法と加減法 バカでもわかる 中学数学

いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者

方程式の種類と解き方 中学で学習する方程式ってどんなのがある 中学数学 理科の学習まとめサイト

1

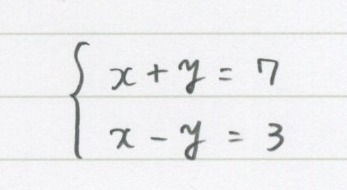
5 1 連立方程式 基本 勉強できようサイト

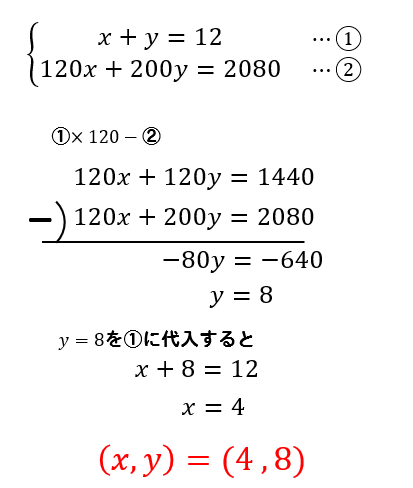
連立方程式の利用 文章問題 解き方まとめ 方程式の解き方まとめサイト

連立方程式の加減法 大人の学び直し算数 計算のやり方解説 無料

連立方程式を小学生に教える

中学２年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

中２連立方程式の解き方と計算問題 代入法と加減法 Irohabook

第4回講義 基礎数学 数学入門

数学 中2 19 ややこしい連立方程式 Youtube

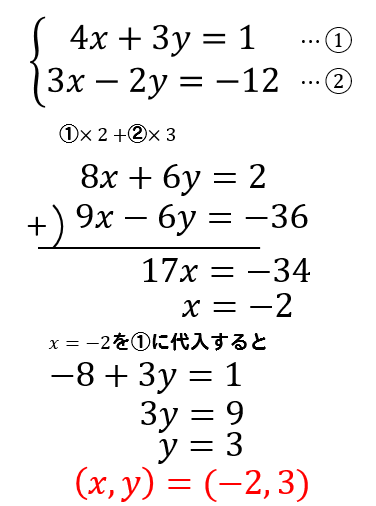
連立方程式 加減法 代入法の簡単な練習問題 これでテストはバッチリ 数スタ

中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット

中学2年 数学の連立方程式の問題です たしかめ4 と問3のやり方 答 数学 教えて Goo

中２ P 52 連立方程式の計算特訓 Youtube

連立方程式の2つの解き方 代入法 加減法 数学fun

4元連立方程式を解く際に気をつけるべきポイントは何でしょうか Clear

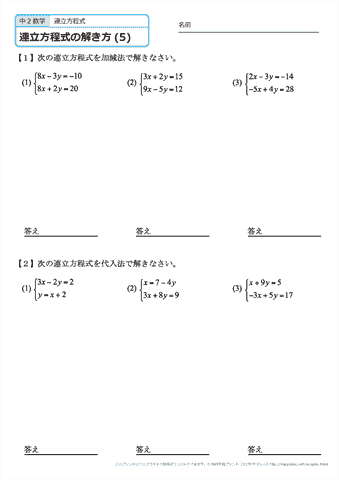
中学２年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

3分で分かる 式が3つの連立方程式の解き方をわかりやすく解説 合格サプリ

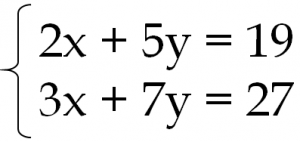
中2数学 連立方程式 代入法はこの3パターンで完璧 たけのこ塾 勉強が苦手な中学生のやる気をのばす

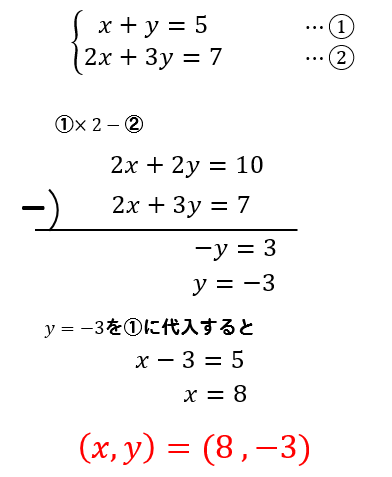
方程式練習問題 連立方程式 A B C 方程式の解き方まとめサイト

第１章 連立方程式

この連立方程式のやり方を教えてください Yahoo 知恵袋

連立方程式 代入法 計算ドリル 問題集 数学fun

たかが連立方程式ではあるけれど 大験セミナー わくわく日記

これを A Bについての連立方程式として解くと これってどうやるんですか Clear

連立方程式の解き方 加減法 Youtube

分数の連立方程式 解き方は両辺に数をかけて分母を消すんだ 中学や高校の数学の計算問題

中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット

2元連立方程式のやり方が分かりません 教えてください 空 Yahoo 知恵袋

いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者

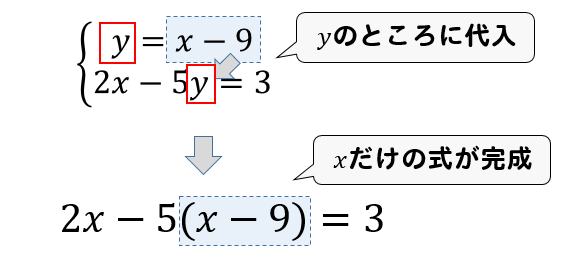
連立方程式 代入法を使った問題の解き方は やり方をイチから解説 方程式の解き方まとめサイト

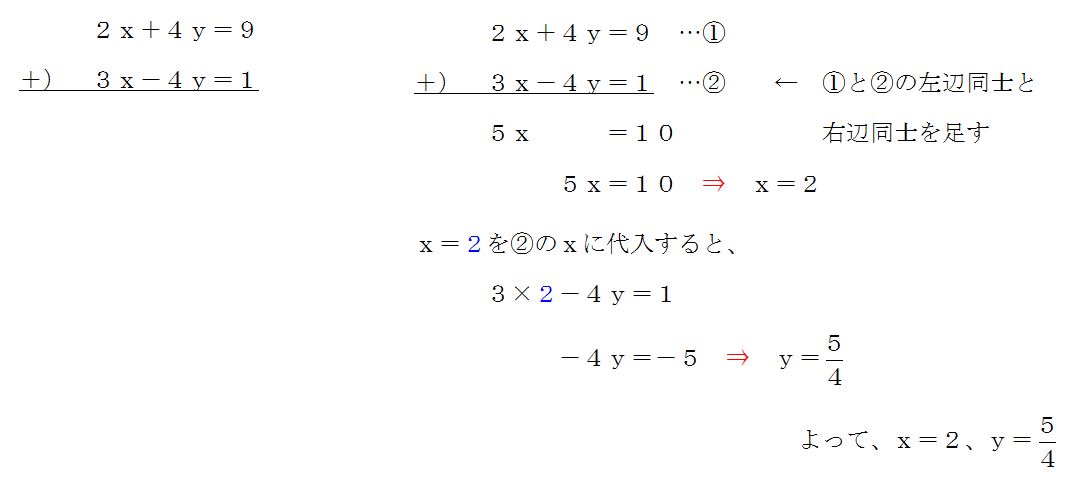
連立方程式の解き方 問題の文字を消すことが解き方のコツだ 三重の個人契約家庭教師

一次方程式 連立方程式 ルートの計算

連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料

3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく

連立方程式の加減法 大人の学び直し算数 計算のやり方解説 無料

このような分数の出てくる連立方程式のやり方を教えてください Clear

5 1 連立方程式 基本 勉強できようサイト

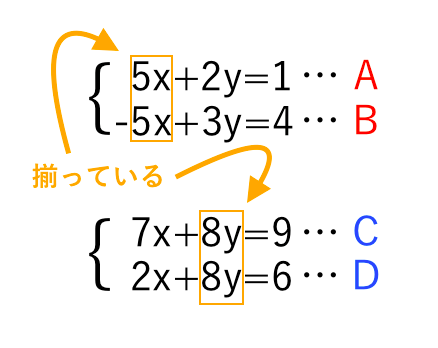
連立方程式の解き方 加減法 苦手な数学を簡単に

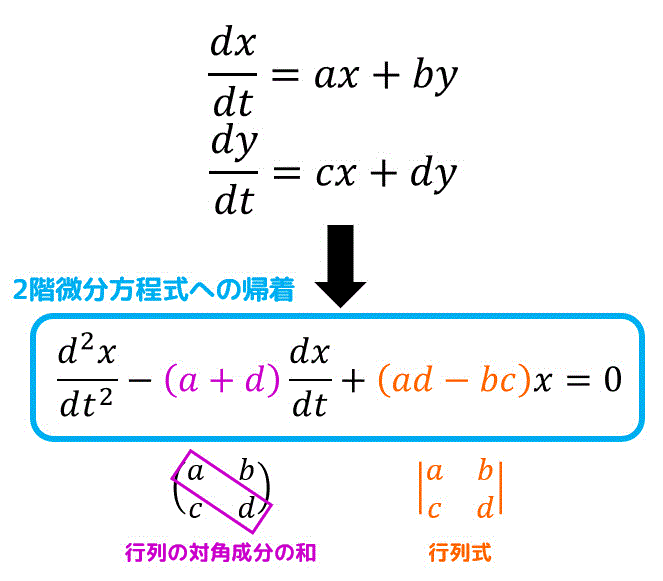
うさぎでもわかる微分方程式 Part10 連立微分方程式 2階微分方程式に帰着させて解くパターン 工業大学生ももやまのうさぎ塾

解き方 連立方程式の加減法がわかる4つのステップ Qikeru 学びを楽しくわかりやすく

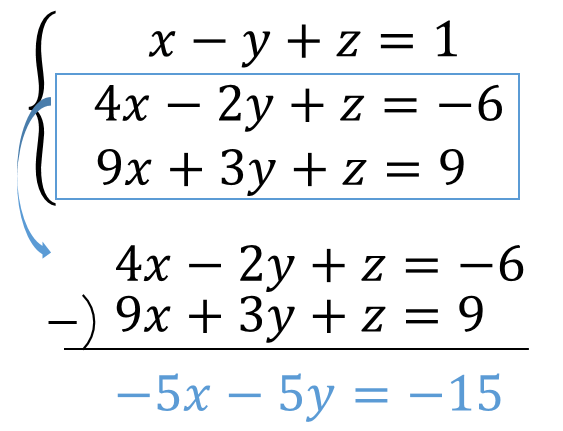
連立方程式 3つの文字 式の問題を計算する方法は 数スタ

連立方程式です やり方を教えて頂けませんか Yahoo 知恵袋

連立方程式の解き方を徹底解説 中学数学からセンター試験まで Studyplus スタディプラス

Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

大まかな解き方だけで 途中式はなくても良いのでこの連立方程式のやり方教えて下さい Clear

数学 中2 15 連立方程式 加減法の基本編 Youtube

連立方程式の加減法の解き方をマスターしたい方は見てください 中学や高校の数学の計算問題

連立方程式の解き方 加減法 代入法と文章題の計算方法 リョースケ大学

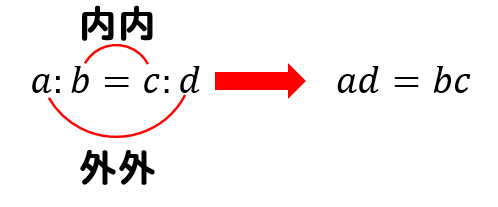
連立方程式 比を含んだ文章題の解き方は 数スタ

連立方程式の解き方 Youtube

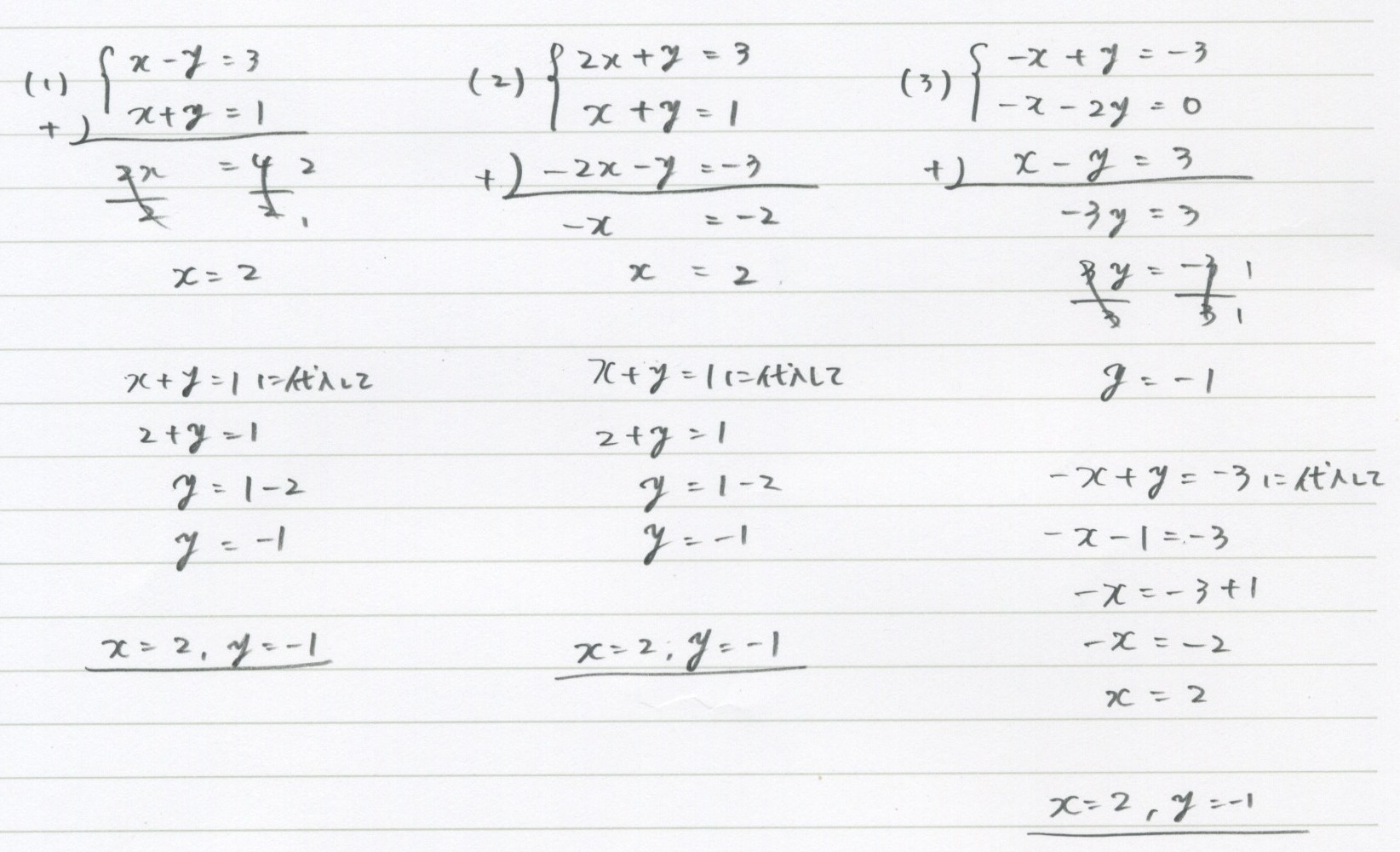
5 1 連立方程式 基本 勉強できようサイト

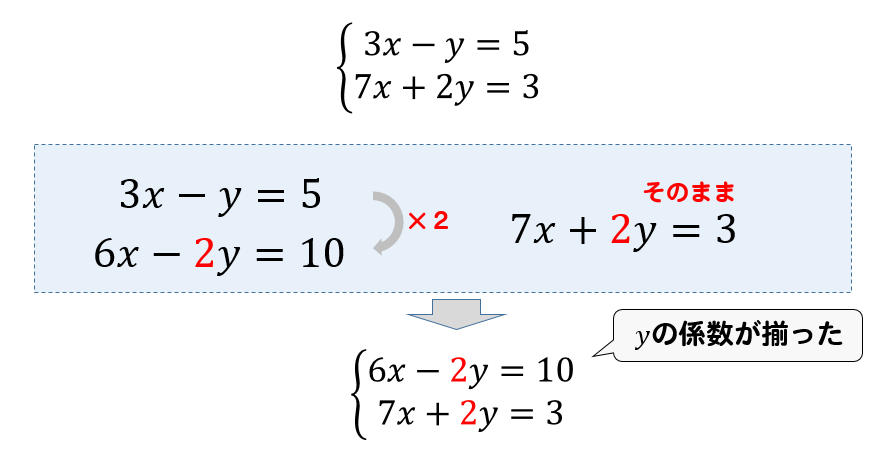
連立方程式 加減法を使った問題の解き方は やり方をイチから解説 方程式の解き方まとめサイト

タカタ先生 タカタ学園 昨日の たしかにひきつける 数学小ネタ集 完成記念トークライブありがとうございました イベントで紹介した連立方程式 の新しい解き方 二重らせん法 の動画を作りました いつかこのやり方が教科書に載る事を夢見てw T

高校数学 2元2次連立方程式3パターン 受験の月

徹底解説 連立方程式の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

連立方程式の解き方 思考力を鍛える数学

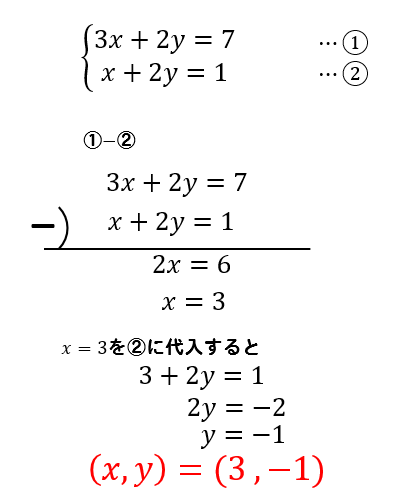
方程式の高校入試問題 連立方程式 方程式の解き方まとめサイト

A Bについて連立方程式で解くやり方を教えてください 赤 Yahoo 知恵袋

解き方 連立方程式の加減法がわかる4つのステップ Qikeru 学びを楽しくわかりやすく

第4回講義 基礎数学 数学入門

連立方程式の加減法 大人の学び直し算数 計算のやり方解説 無料

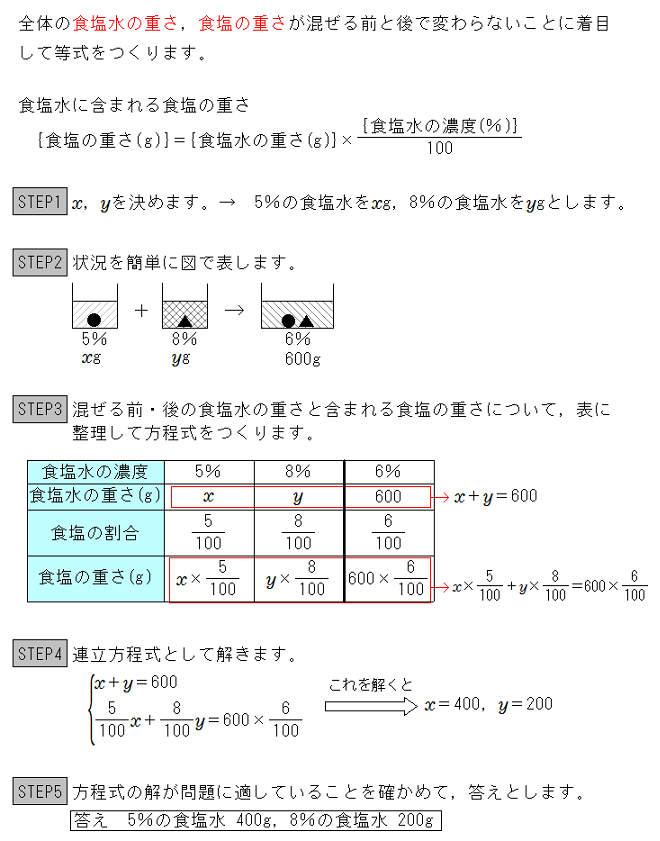
連立方程式 食塩水の問題で連立方程式をつくるコツ 中学数学 定期テスト対策サイト

Incoming Term: 連立方程式のやり方,