図形の美しい3つの定理〜逆数の和〜 逆数の和に関する平面図形の美しい定理を3つ紹介します。実用的な定理ではありませんが,証明はよい練習問題になるのでトライしてみてください! → 図形の美しい3つの定理〜逆数の和〜1 単元名 図形の面積〔B(3)平面図形の面積〕 2 指導観 (1)教材観 本単元は,平行四辺形や三角形などの直線で囲まれた基本的な図形の面積の求め方について,長方②分割した長方形の面積を求めます。 a=5m×2m=10㎡ b=2m×4m=8㎡ c=10m×2m=㎡ ③X軸、Y軸から中心(図心)まで距離を求めておきます。 Xa=7m Xb=4m Xc=1m Ya=25m Yb=1m Yc=5m では、計算しましょう。
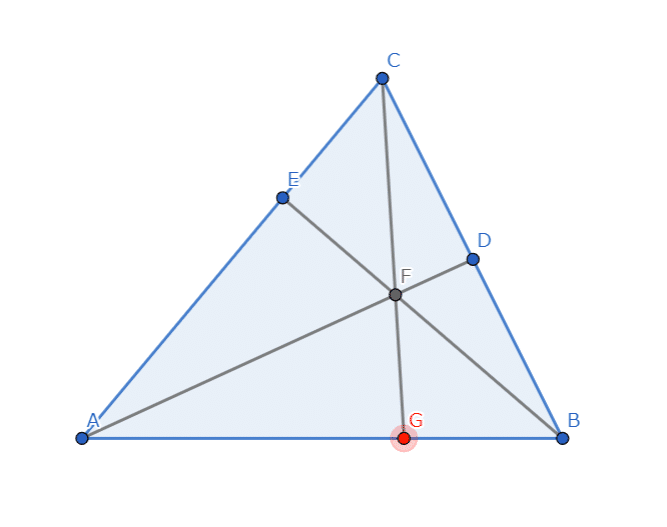
平面図形 三角形を分割した時の底辺の比とコンパスのような部分の面積の比は同じ ワンセンテンス算数 Note
平面図形の面積 細案指導案
平面図形の面積 細案指導案-平面図形の難問1(12日大豊山中) 図のように,1辺の長さが18cmの正方形ABCDと,角アが90 の直角二等辺三角形があります。このとき,三角形BEFの面積を求めなさい。 (印刷する場合は平面図形の難問1(12日大豊山中)PDFへ) この記事では、図形の面積を求める際に必要な考え方・ テクニックを簡単にまとめます。 図形の公式等、平面図形の面積の基本については上記記事を 読んでください。ただし、この記事のレベルはまだ「基本」 となります・・・。
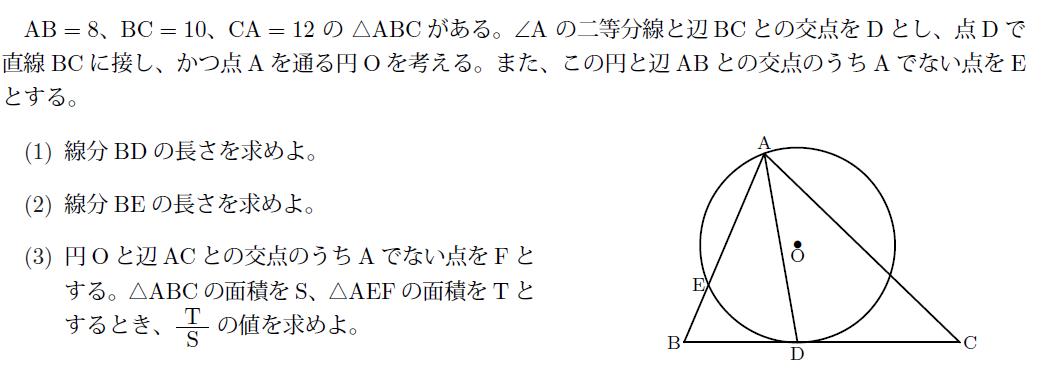



平面図形の面積比に関する問題です F1 数学 箱根駅伝ブログ
平面図形「ひし形の面積は、一方の対角線×他方の対角線÷2、正方形の面積は、対角線×対角線÷2」 オンライン家庭教師はじめました。 ③ 上記ホームページ の下の方にに私宛のメッセージ機能(STEP1として「ワンセンテンス算数さんにメッセージを送る平面図形面積(発展) 2③解説 影をつけた部分の面積を求めよ。 ③ 4cm 4cm 影の部分は図の赤い部分と同じものが4つでできている。 2cm 2cm 2等分 さらに赤い部分を2等分した図形の面積を求める。 この部分は半径2cm、中心角90 の 18年東京都で行われた公立入試中学受験 算数 動画解説 平面図形13 面積③ 三角形の面積3 制作者のホームページは http//kyoikuinfo
ベクトルと平面図形01 位置ベクトル 内分 外分 ベクトルと平面図形02 内分、外分の公式 ベクトルと平面図形03 外分の公式は#平面図形に関する一般一般の人気記事です。''答動画数学難問 正答率01% 北辰テスト 一次関数、平行線と面積''三女幼稚園時代の習い事⑤ 花まる学習会''問題が解けない間違えるときの親の姿勢について''算数、数学の立体図形分析 学習方法②''中学入試期間中の家庭学習 〜 算数編 〜 中学受験 算数 平面図形の面積 ~成り立ちから詳しく解説~ 中学受験の算数で出題される重要単元「平面図形」。角度や辺、面積を求めたり、比で表したりします。この単元では、図形の性質と基本公式をしっかり覚えておくことがポ
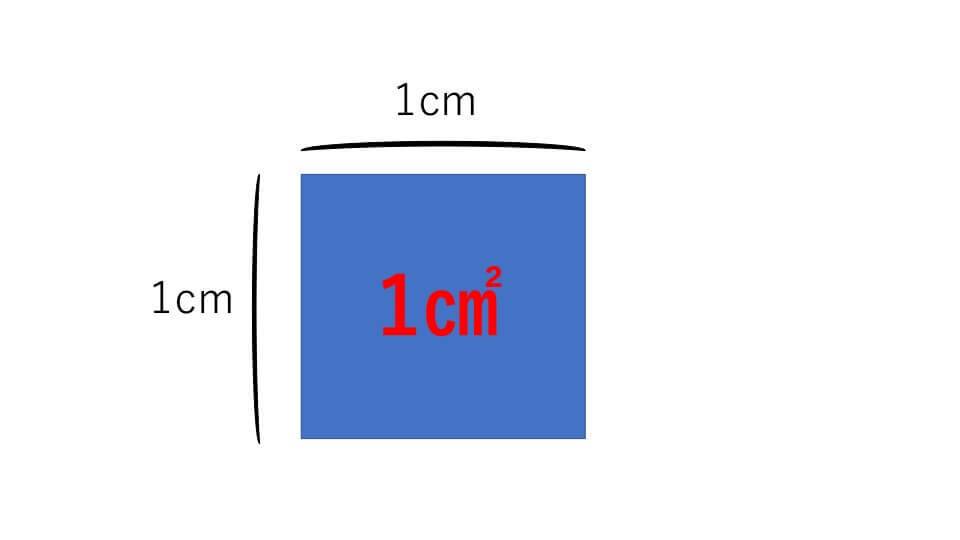
面積 めんせき 線で囲まれた平面の一部分の広さのことをいう。 平面図形dの面積というのは、一辺の長さ1の正方形の面積を1としてdがその何倍にあたるかを示すものである。 面積の計算の原理は次のようになっている。 〔1〕二つの平面図形d 1 、d 2 をあわせてできる平面図形の面積はd 1 、d 2平面図形の性質 P12 立体の体積(V),表面積(S)または側面積(F)および重心位置(G) P12 平均自乗誤差 P13 円板の最大応力(σmax)と最大たわみ(ωmax) P96 長柱の座屈 P97 各種断面形の軸のねじり P97 梁の公式 P98 キーの強さ P102 平面図形の面積(小5算数) 算数 今回の算数は平面図形の3週目で「平面図形の面積」。 4年の復習が多いように思えますが、娘には願ったり叶ったり。 ここでのポイントは、 三角形の高さを見つける練習、 面積の等しい三角形を探す練習、 です




つまずきをなくす小4 5 6算数平面図形 角度 面積 作図 単位 通販 セブンネットショッピング
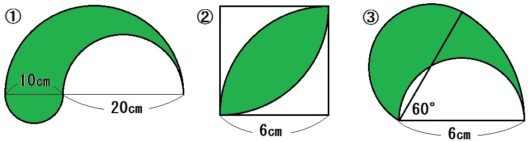



中学数学 平面図形 のコツ 円とおうぎ形
平面図形 例題 基本の作図(垂線) 基本の作図(垂直二等分線、角の二等分線) 作図 正三角形,円の中心 作図 角度60°,30°,45° 作図 角度75° 作図 平行線 円の接線 作図 三角形の3頂点を通る円, 三角形の3辺に接する円 おうぎ形_半径と中心角から弧の長さや,面積を求める おうぎ形2_半径と弧から,面積を平面図形の幾何学と歴史 山岡 緑 高知工科大学マネジメント学部 1.概要 ていた。 5.2本研究では、定理の起源に迫ることで、より理解を深める ことを目的とする。小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題
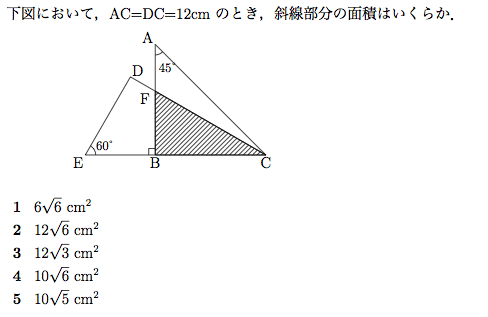



平面図形 面積 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください
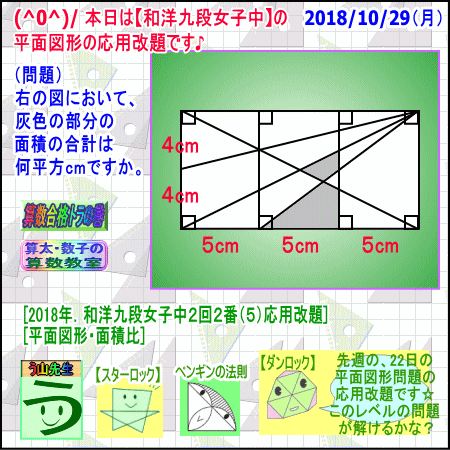



平面図形 面積比 和洋九段女子中改題 2018年 算数 数学 受験 中学受験 算数プロ家庭教師 算数合格トラの巻 エキサイト ブログ
投稿者 桜組 時刻 17時09分 算数 平面図形・面積の問題, 開成中学 固定リンク Tweet « 平面図形の長さ 第23問 (雙葉中学 受験問題 13年(平成25年度) 算数) トップページ 平面図形の長さ 第24問 (鎌倉学園中学 入試問題 07年(平成19年度) 算数) »1年生 5 平面図形 知識ヹ技能の習得を図る問題 年 組 号 氏名 練習問題② 次の(1)から(4)までの各問いに答えなさい。 (1) 右の図は,佐賀県のシンボルマークで, 線対称な図形です。この図形の対称の軸を かき込みなさい。れぞれ半分に切って4つの図形に分ける(平面図形の 場合).そして,その4つの部分それぞれについて性 質を調べる.この手順を図形それぞれが十分に小さく なるまで繰り返す方法である. この問題の場合,分割統治法によって近似面積を求
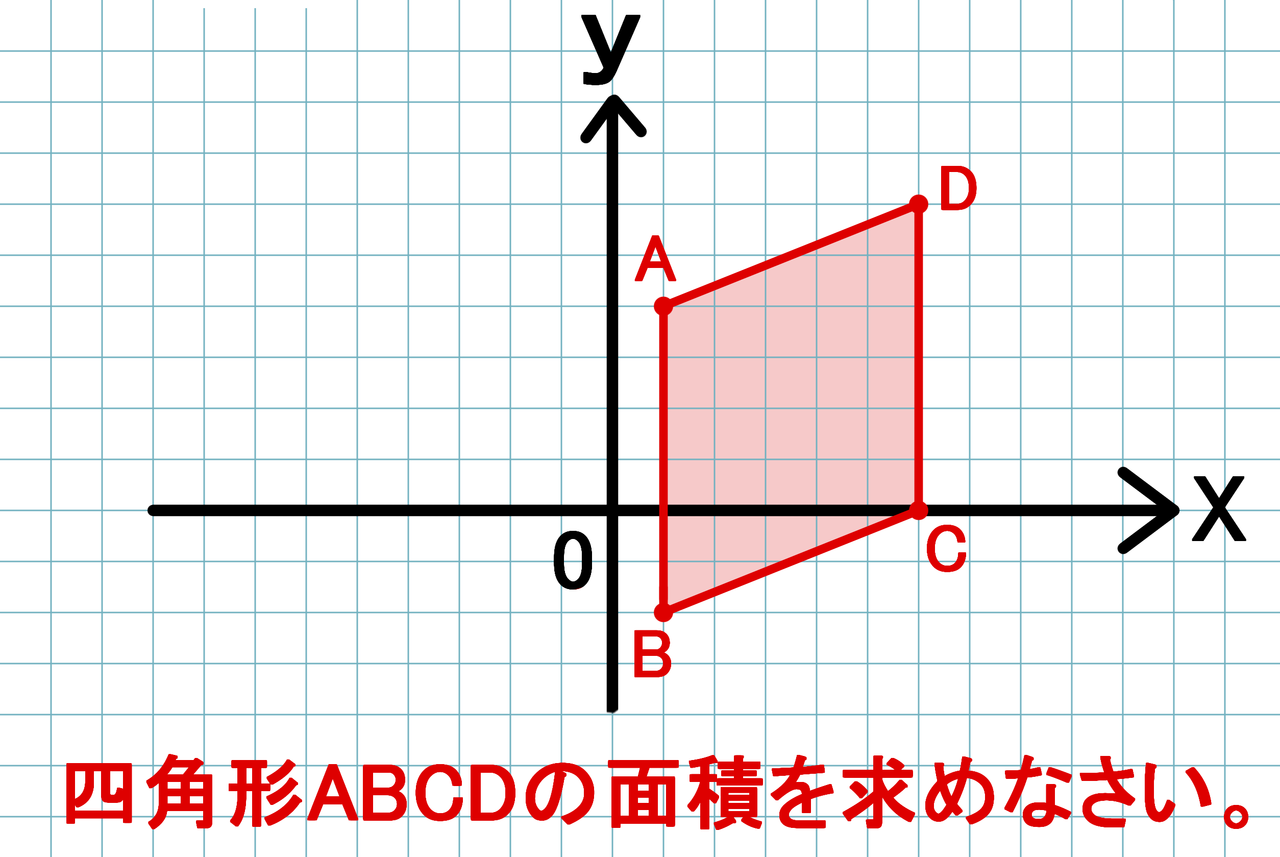



座標平面に描かれた図形に関する問題 バカでもわかる 中学数学
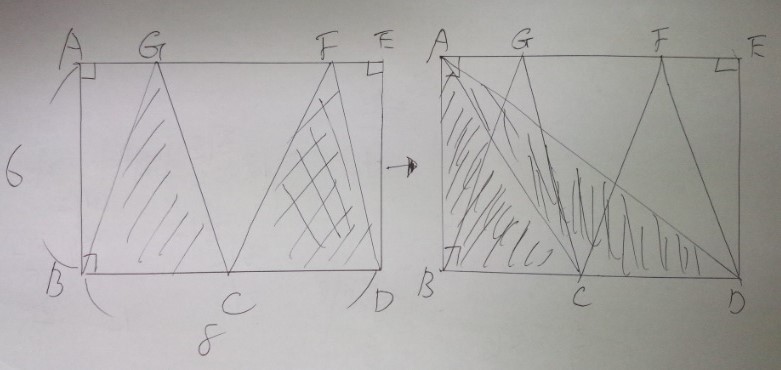



平面図形 多角形 円
5 「図形の面積」 1 出題の趣旨 基本的な平面図形の面積の求め方を理解しているかどうかをみる。 この問題は,平行四辺形や三角形,円の面積の求め方を理解し,面積を求めることがで きるかどうかをみるものである。5年生向け 成城学園中学校09 平面図形 解いた経験がなければ手強い問題かもしれません。 フィードバック (不具合・誤記・問題解法の矛盾に関する連絡) ご利用頂きまして誠にありがとうございます。 ご記入頂いた内容は完全に非公開です。 みんなのこちらはよく質問をいただく図形です。 初見では難しいかもしれませんが、 図形の見方を覚えてしまえば楽勝です。 面積を考える場合には、 次のように8等分した部分の面積を考えていきましょう。




第9回 平面図形 長方形 正方形の面積 4年生 日能研の歩き方
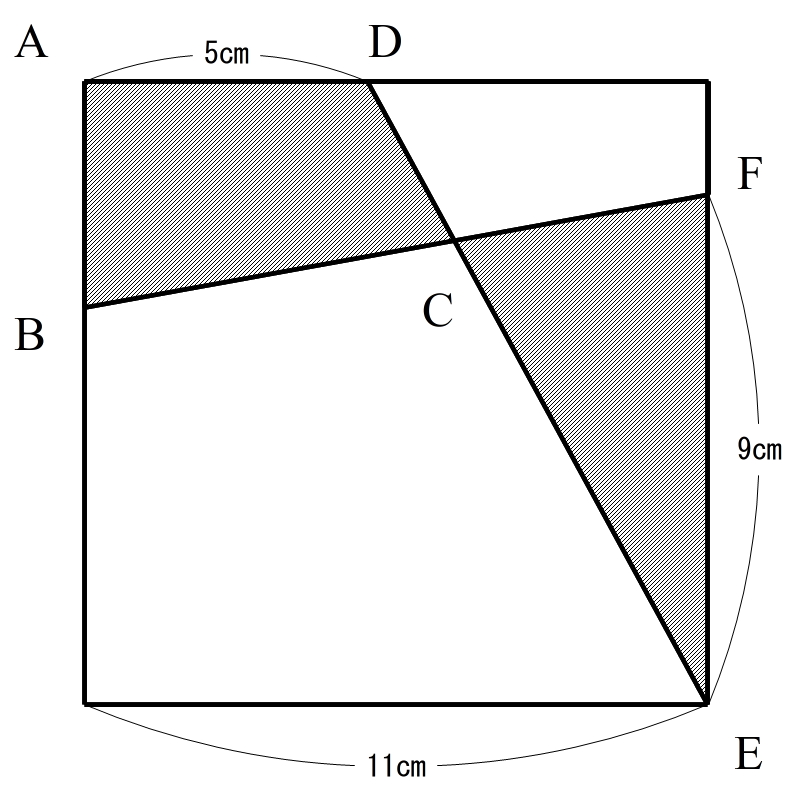



等積な平面図形 女子学院中 14 中学受験入試標準問題集 今日の1問
面積 (めんせき)とは、平面内の、あるいは曲面内の図形の大きさ、広さ、の 量 である。 立体 物の表面の面積の合計を特に 表面積 (ひょうめんせき)と呼ぶ。入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 直角三角形 4年生 女子校 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 ファイナル 二等辺平面図形・面積 (発展) 2 2 影をつけた部分の面積を求めよ。 ① 5cm 4cm 3cm ② 4cm 3cm 72° ③ 4cm 4cm 影をつけた部分の面積 全体から引く ① 外側の円の直径は 345 =12 なので半径6cm よって面積は6×6×π =36π 中の白い円は直径が順に3,4,5なので




中学3年の三平方の定理と平面図形です この問題の台形の面積を求めてください Clear




数学 面積比と線分比をシッカリわかると チェバの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生
複素数平面における三角形の面積 I m z \mathrm {Im}z Imz は複素数 z z z の虚部を表しています。 任意の複素数 z z z に対して I m z = z − z ‾ 2 i扇形の弧の長さと面積 平面図形 公式集 確認シート a =長さ b =長さ h =高さ ℓ =弧の長さ S =面積 V =体積次の図形の黒くぬった部分の面積を求めなさい。 → 解答 問題3 次の図形の黒くぬった部分の面積を求めなさい。 → 解答 問題4 三角形ABCの面積が85c㎡のとき、三角形ADEの面積を求めなさい。ただし、辺BCは5等分されています。 → 解答




はっぱ型 の図形の面積 身勝手な主張
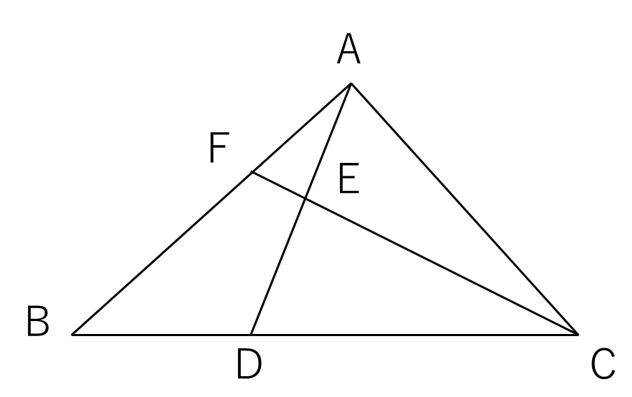



三角形の面積比をてんびんで解く 中学受験プロ講師ブログ
学ぶ・教える.com > 中学受験 > 算数 > 平面図形の面積 > 空白の部分をはしに寄せて、黒くぬった部分を集めると、右の図のようになる。 求める面積は、 円周=直径×円周率(314)=半径×2×円周率(314) 円の面積=半径×半径×円周率(314) おうぎ形の弧の長さ=円周×中心角/360=直径×314×中心角/360 おうぎ形の面積=円の面積×中心角/360=半径×半径×円周率×中心角/360中学受験 4年 unit 312 平面図形‐面積2 面積と長さ どれを底辺にするか。 直角三角形の高さを求める。 4年生向け 中学受験 算数 面積と長さ どこを底辺と見るか。 例題とともに解説します。 If playback doesn't begin shortly, try restarting your device Videos




面白い算数問題 中学受験 中学入試 算数 解説 平面図形 面積 Youtube
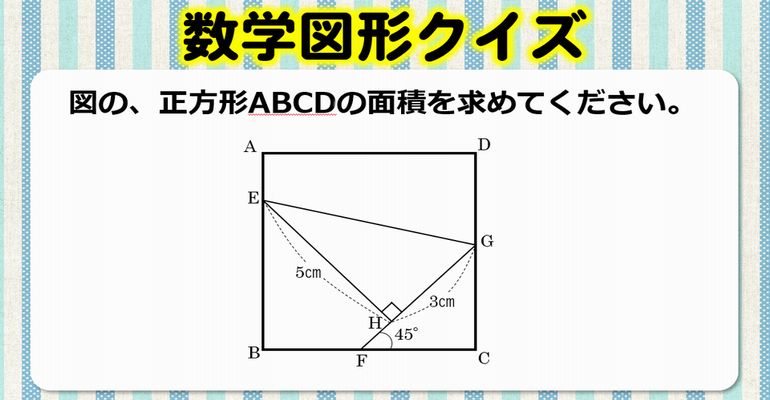



数学図形クイズ シンプルだけどひらめきが必要な正方形の面積の良問 ネタファクト
算数「平面図形の面積と角度」中学受験 中学受験 問題6 右の図1の二等辺三角形を、図2のように3つおいたとき、アの角度は何度ですか。 (早稲田中 08年) <問題6の考え方と答え> まずは、次のように、図にA~Gまで点をつけました。 同じ二等辺No029 平面図形 灘中模試 30度 6年生 おうぎ形 正方形 灘 ★★★★★☆(算オリ・灘中受験生レベル) 灘中学校を目指している受験生のために。 1日目2枚目(図形問題の単問)の予想問題をオリジナルで作成しております。多角形の座標入力で簡易に面積計算出来るので役に立つ。 アンケートにご協力頂き有り難うございました。 送信を完了しました。 座標点で囲まれる多角形の面積 のアンケート記入欄 性別 男 女 年齢 歳未満 歳代 30歳代 40歳代 50歳代 60歳以上
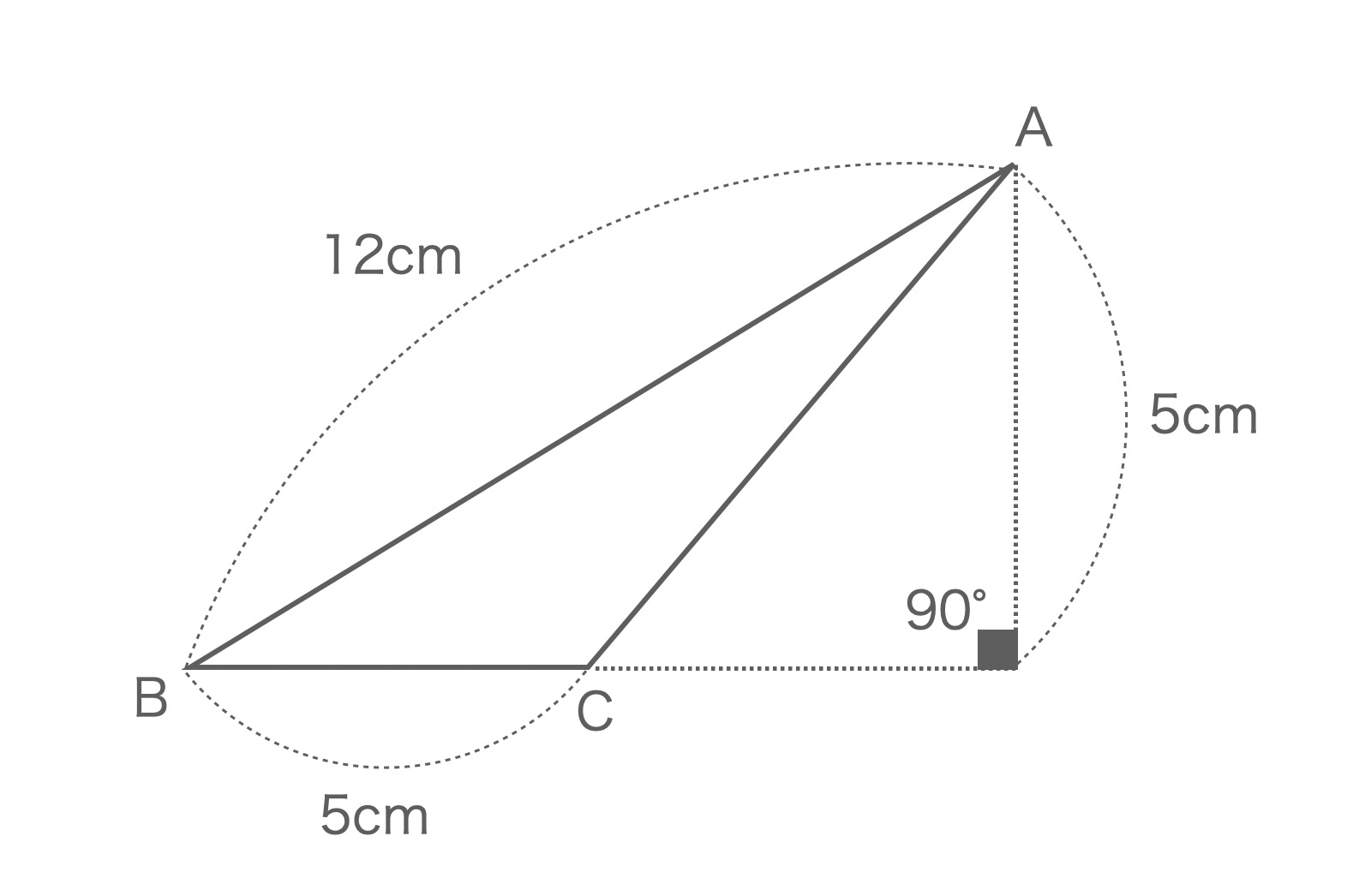



平面図形 面積を求める問題 の基礎 カテキョウブログ




中学数学平面図形 公立高校入試の良難問 定期テストや高校入試に レオンの中学数学探検所
採点する やり直す 解説 3 半径 10 ,中心角が90°の扇形の面積 円の面積の4分の1だから,10 2π ÷4=25 π π 採点する やり直す 解説 4 下の図の灰色で示した図形の面積 扇形の面積は円の4分の1で25 π ,これから三角形の面積 10×10÷2=50 を引く



面積 これが中学入試に出た図形問題




平面図形をマスター 三角形の面積比 応用編その2




5年生で 様々な図形の面積の求め方を習いますが ここでは 平行四辺形と三角形の面積の求め方を学習する自主学習ノートの例を紹介します 平行四辺形と三角形の面積を求める 三角形の面積 学習 学習ノート 子どもたちの研究




東大寺中2017年 平面図形ー 中学受験算数の良問 難問 基本問題




平面図形の面積の求め方 基本編 中学受験 塾なし の



無料 中1数学 テスト対策問題 問題プリント 127 平面図形3 実力アップ




平面図形をマスター 三角形の面積比 応用編その3




面積の求め方 算数の教え上手 学びの場 Com




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学




この図形の面積の求め方を教えてくださいm M Clear
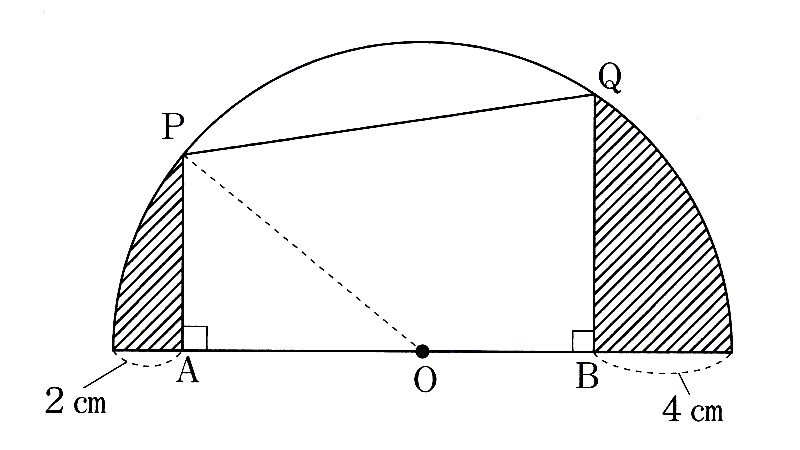



北辰塾 情報局 直撃 中学入試問題 第346回 大妻多摩 平面図形 おうぎ形と台形の面積




六甲学院中2018年 平面図形ー 中学受験算数の良問 難問 基本問題
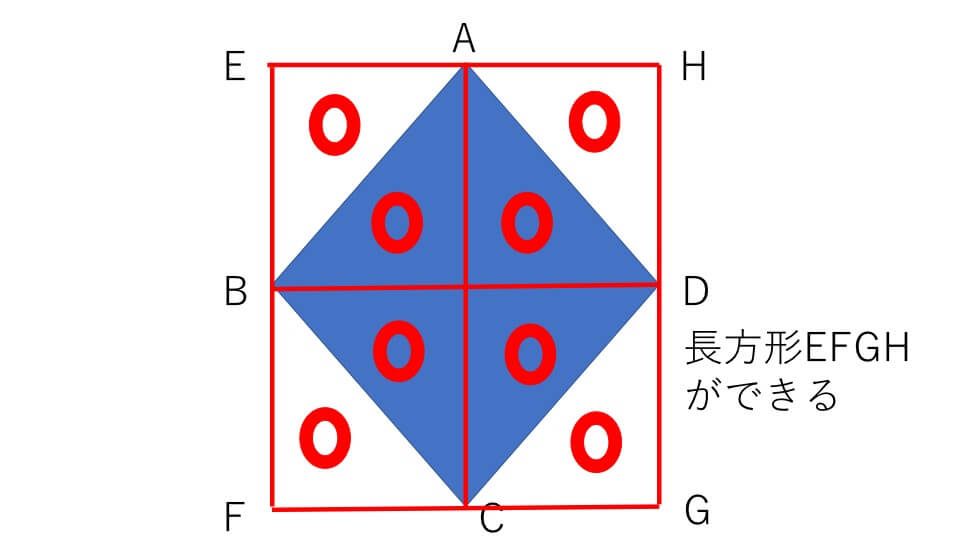



中学受験 算数 平面図形の面積 成り立ちから詳しく解説 中学受験アンサー




トップ校への数学 中1 平面図形 空間図形 17年3月 かなり進学塾オンライン




円の面積 練習応用 Youtube



みんなの算数オンライン 中学受験 4年 平面図形 面積2 面積と角度 トレーニング




辺の比 面積比 相似 16年東京都 高校入試 数学 良問 難問



平面図形 算数解法の極意




高校数学b 三角形の面積のベクトル表示 成分表示とその証明 受験の月
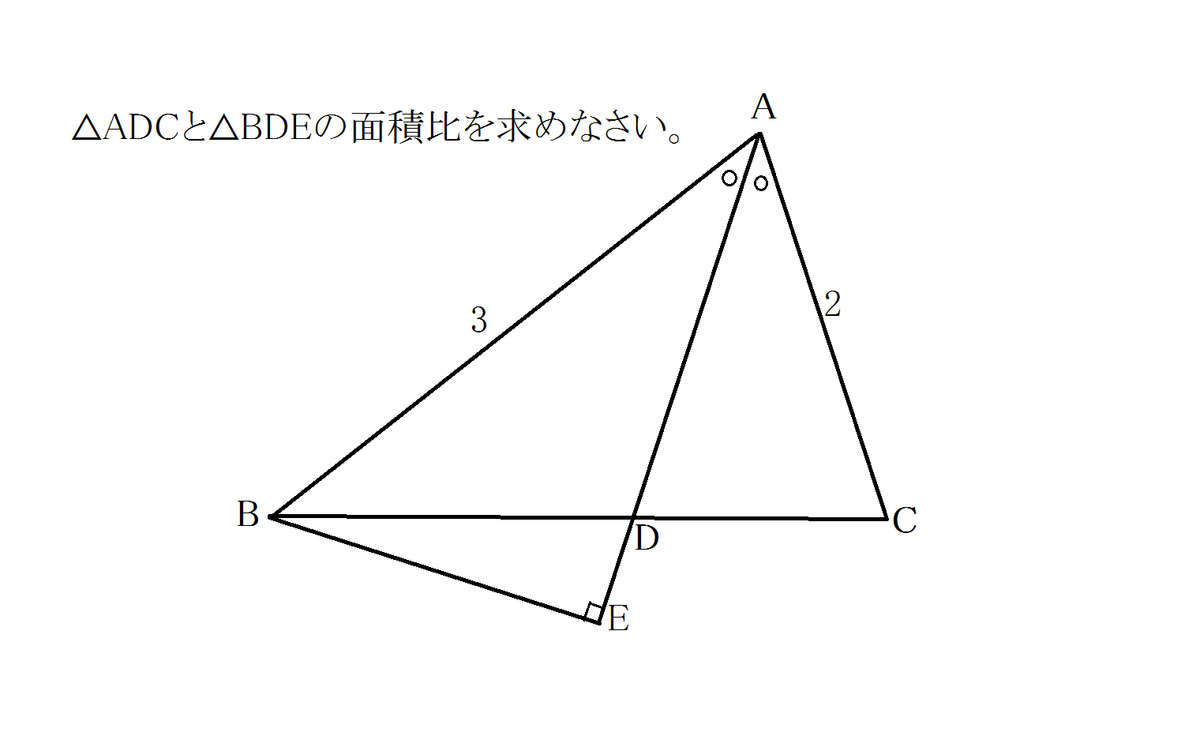



中学数学発展 シンプルだけど難しい ラ サールの難問 平面図形 定期テストや高校入試に レオンの中学数学探検所




円とおうぎ形 応用 無料で使える中学学習プリント




中学受験 算数 平面図形の面積 成り立ちから詳しく解説 中学受験アンサー




中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su



250枚 至急 葉っぱ形の図形の面積について質問です Yahoo 知恵袋




平面図形 三角形を分割した時の底辺の比とコンパスのような部分の面積の比は同じ ワンセンテンス算数 Note




面積の求め方 算数の教え上手 学びの場 Com
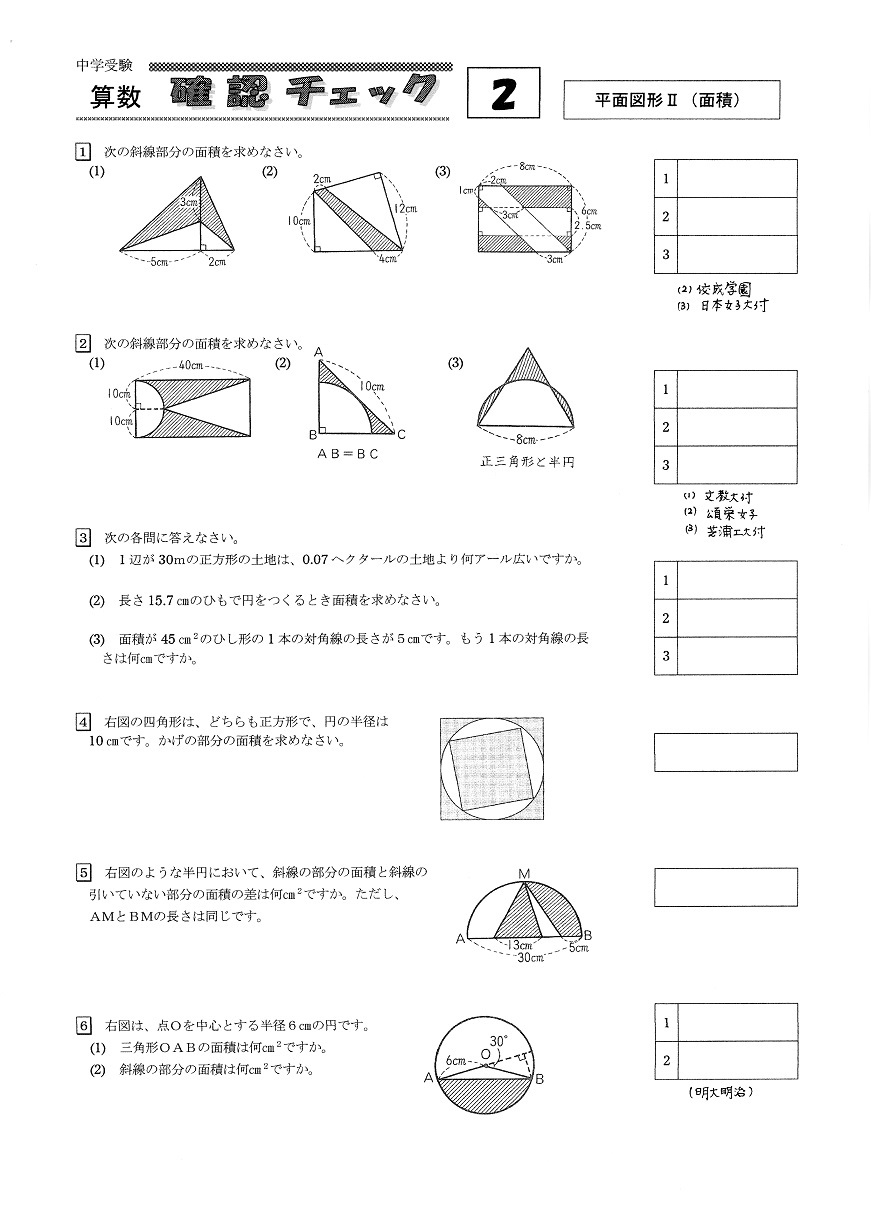



中学受験 算数確認チェック2 平面図形 面積 グランパは元塾長



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




辺の比と面積 平面図形 中学受験の算数 理科ヘクトパスカル
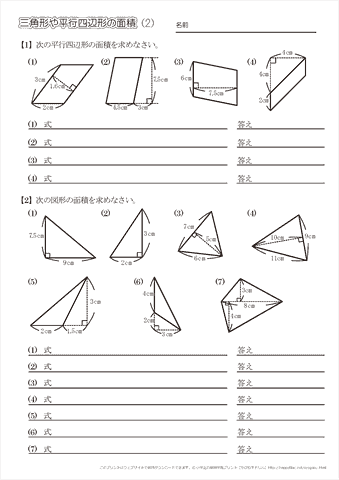



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生



1



算数 テーマ別 ポイント集 平面図形 10 14 中学受験の勉強法 偏差値アップの学習法




なぜ 周の長さの比は 25を使うんですか 下の15cmは使わないんですか Clear
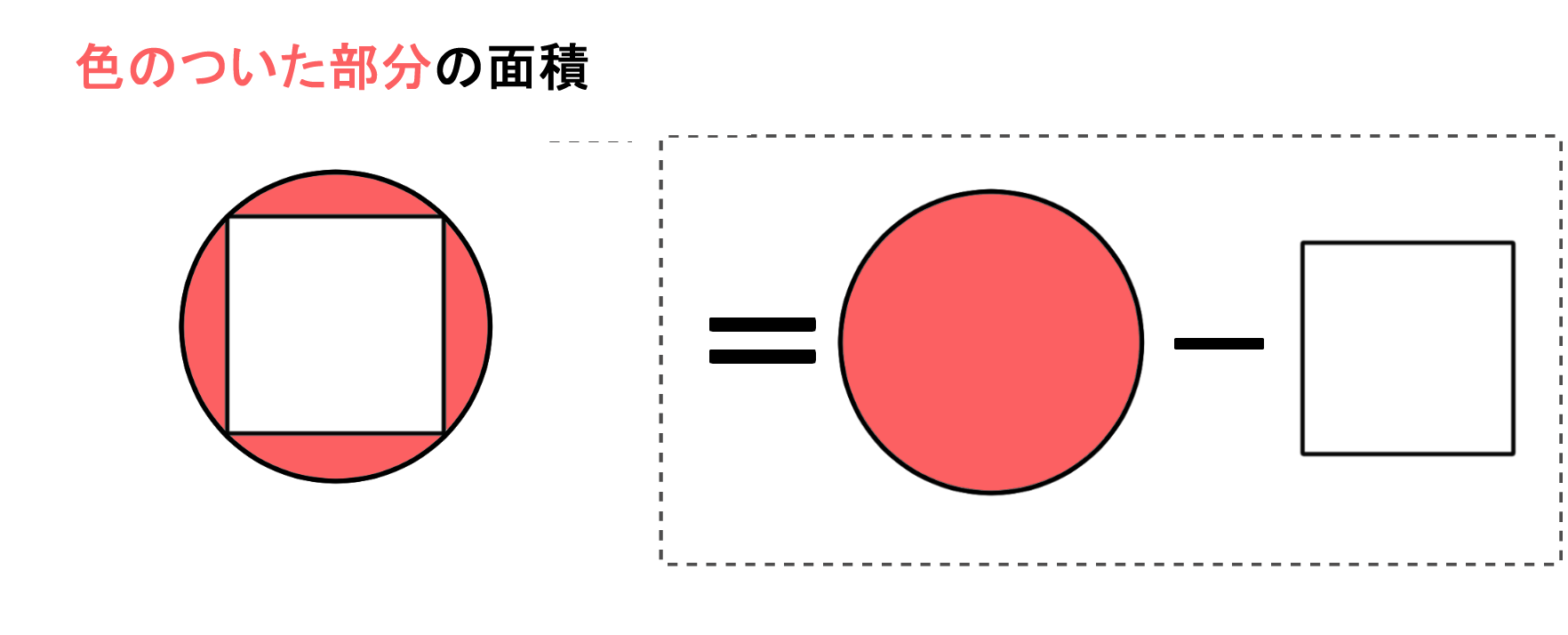



色のついた部分のへんな形の図形の面積を求める問題 バカでもわかる 中学数学




つまずきをなくす小4 5 6算数平面図形 角度 面積 作図 単位 通販 セブンネットショッピング




平面図形の苦手を解消 三角形の面積比 基本編



中1数学 発展 応用問題プリント 平面図形のおうぎ形の弧と面積 138
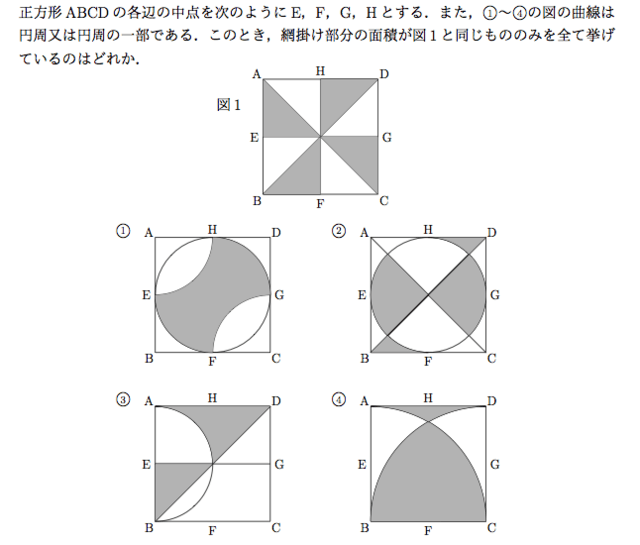



面積移動 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください
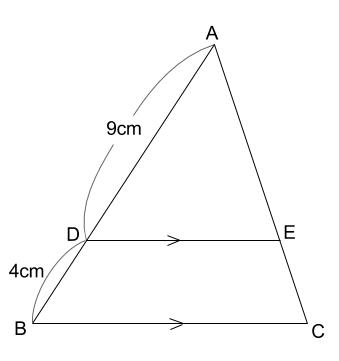



中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su




平面図形の面積比 数学i フリー教材開発コミュニティ Ftext
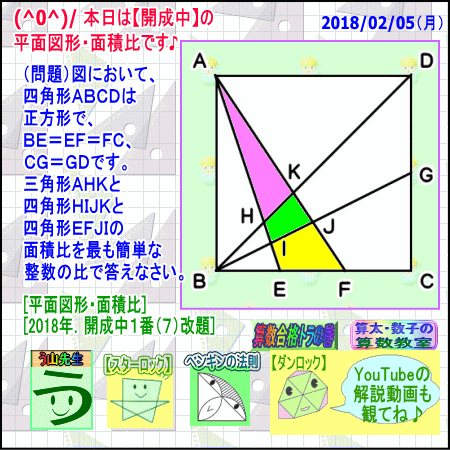



平面図形 面積比 開成中2018年 算数 数学 受験 算太数子 中学受験 算数プロ家庭教師 算数合格トラの巻 エキサイト ブログ



無料 中1数学 基本問題 解答プリント 平面図形5 おうぎ形の弧と面積 138



みんなの算数オンライン 中学受験6年 平面図形 実戦過去問 応用




平面図形と面積 比を究める15題 Myisbn デザインエッグ社 清水良太郎 本 通販 Amazon
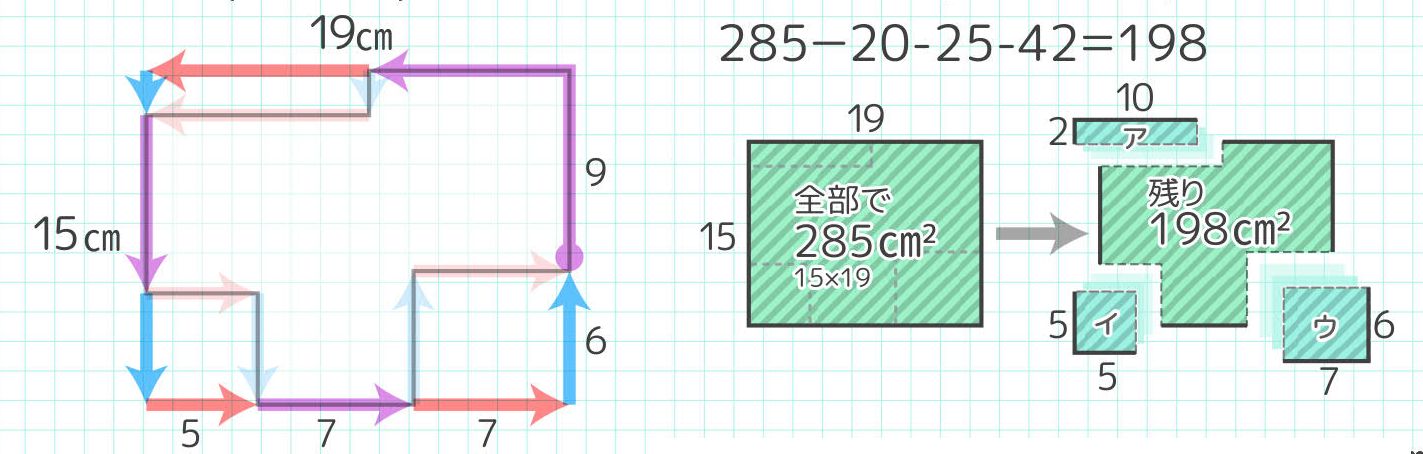



小2から プリント12枚 正方形長方形の面積の求め方と公式 対角線からも 中学受験まで そうちゃ式 受験算数 2号館 図形 速さ



3
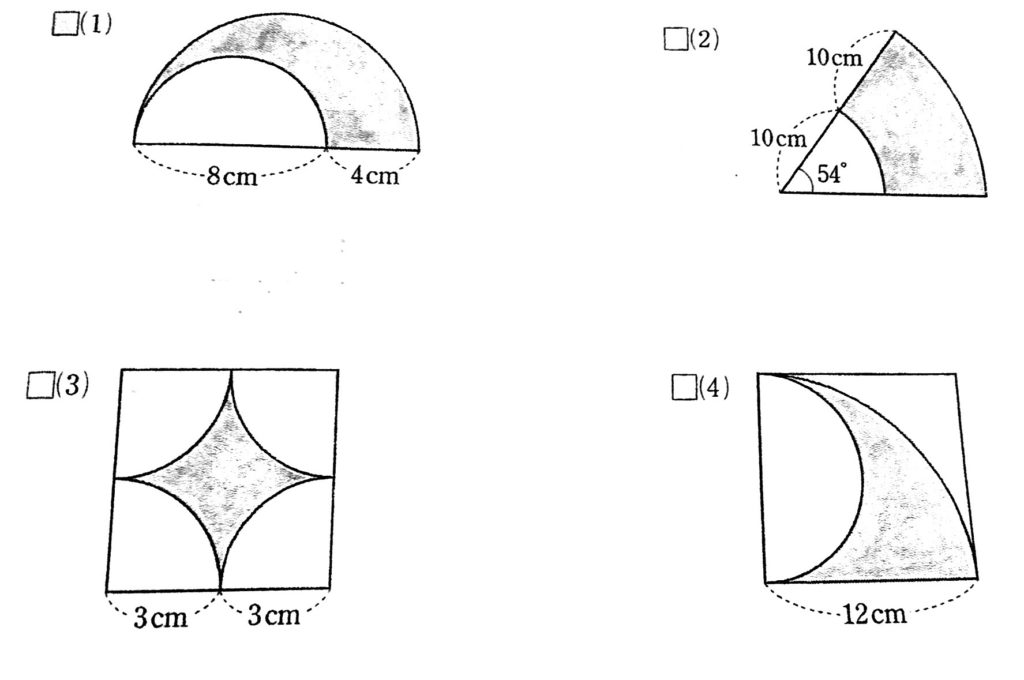



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ
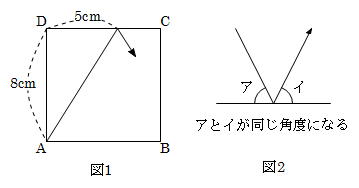



平面図形 辺の比と面積の比 前田昌宏の中学受験が楽しくなる算数塾



3
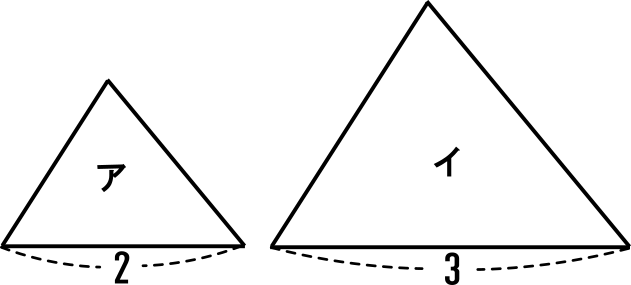



中学3年数学練習問題 相似な平面図形の面積の比 図形と相似




平面図形の面積 まとめ7 8 いろいろな図形の面積 Youtube




メルカリ 平面図形 図形 角度 面積 算数 暗記カード 家庭学習 ラミネート 参考書 399 中古や未使用のフリマ



平面図形の面積 学ぶ 教える com




標準 おうぎ形と正方形の面積 なかけんの数学ノート




2 2 8cm 6 Cm Lihat Cara Penyelesaian Di Qanda




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
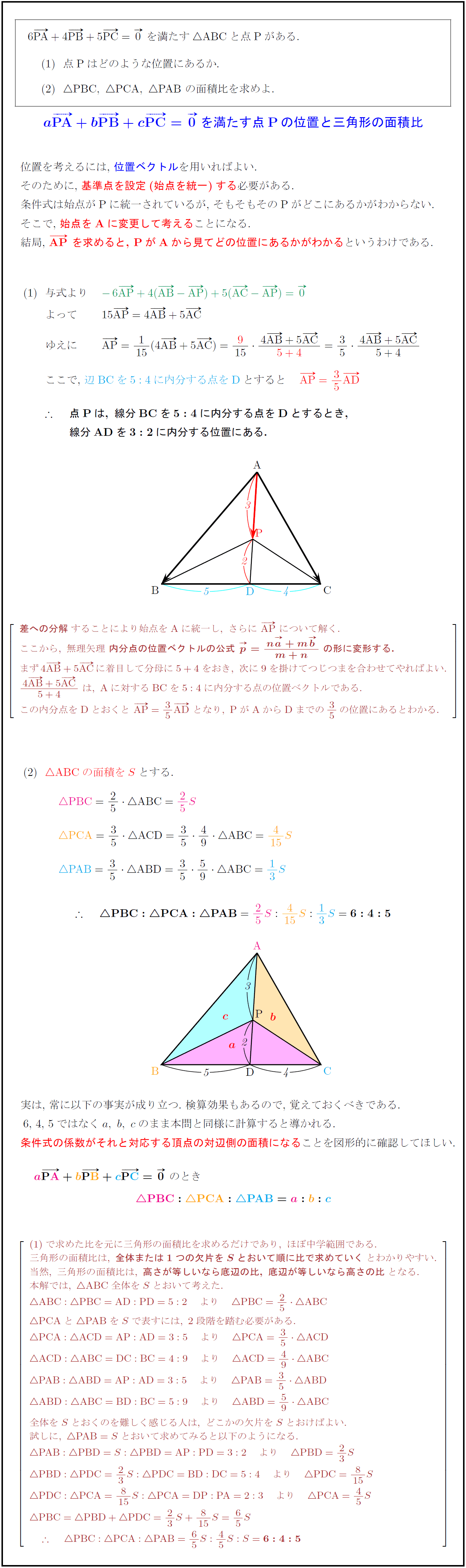



高校数学b Apa Bpb Cpc 0を満たす点pの位置と三角形の面積比 受験の月
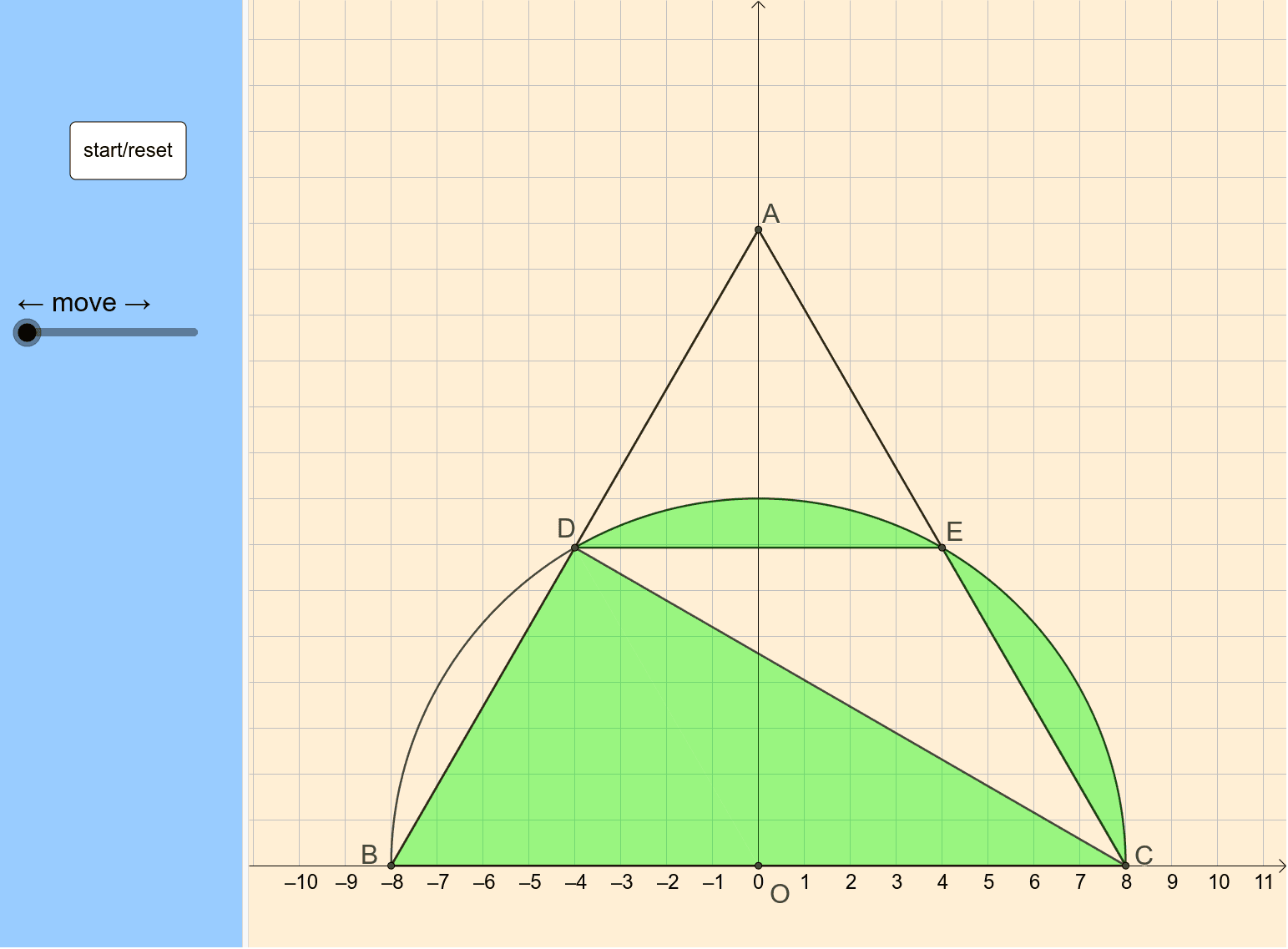



平面図形 円とおうぎ形の面積 Geogebra




算数 平面図形 面積の問題 まいにち一題 中学受験過去問題研究



帝京大学中10 2 の 6 平面図形 複雑な図形の面積を2等分する 気まぐれ解説カフェ 仮
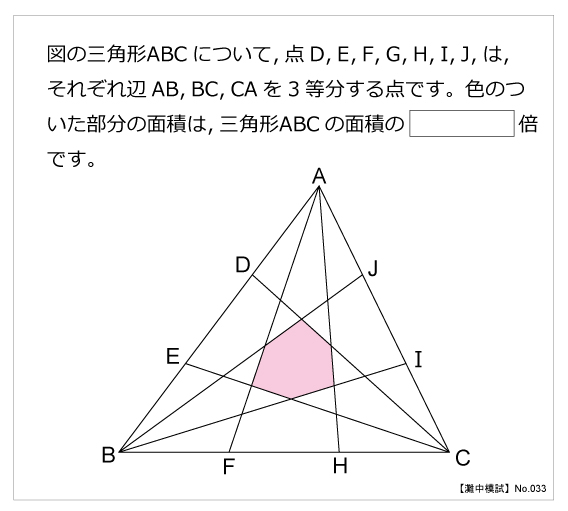



灘中模試 No 033 平面図形 算数星人のweb問題集 中学受験算数の問題に挑戦




平面図形の面積比に関する問題です F1 数学 箱根駅伝ブログ




中1 数学 中1 77 おうぎ形の弧と面積 ややこしい図形編 Youtube



中学受験 算数 平面図形の面積 成り立ちから詳しく解説 中学受験アンサー
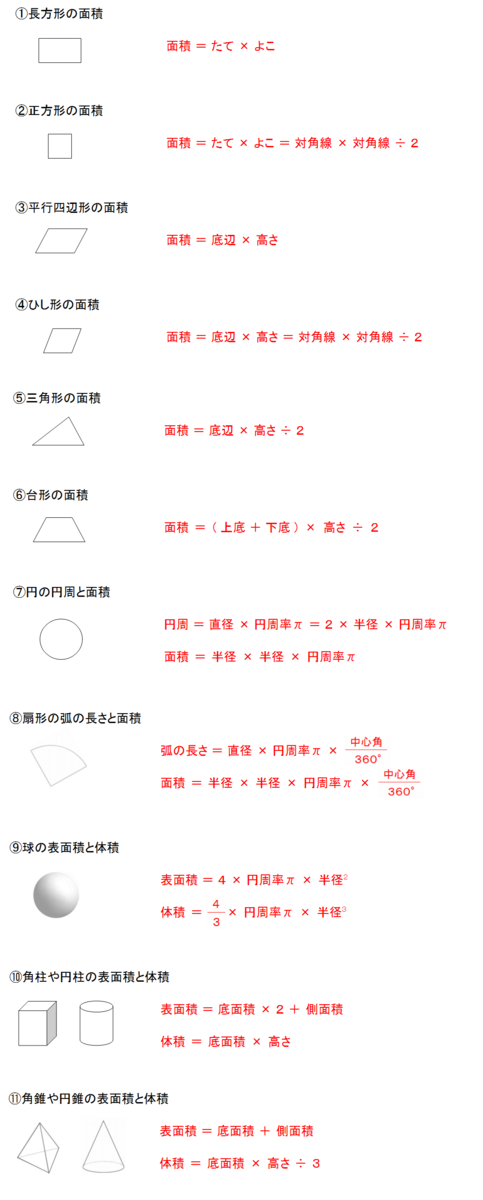



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




平面図形をマスター 三角形の面積比 応用編その2




高校数学 座標平面上の三角形の面積の公式 受験の月




平面図形 面積比 和洋九段女子中 2018年 算数 数学 受験 算太 数子の算数教室 う山先生 の はてなブログ



平面図形の面積 灘 2007 どう解く 中学受験算数
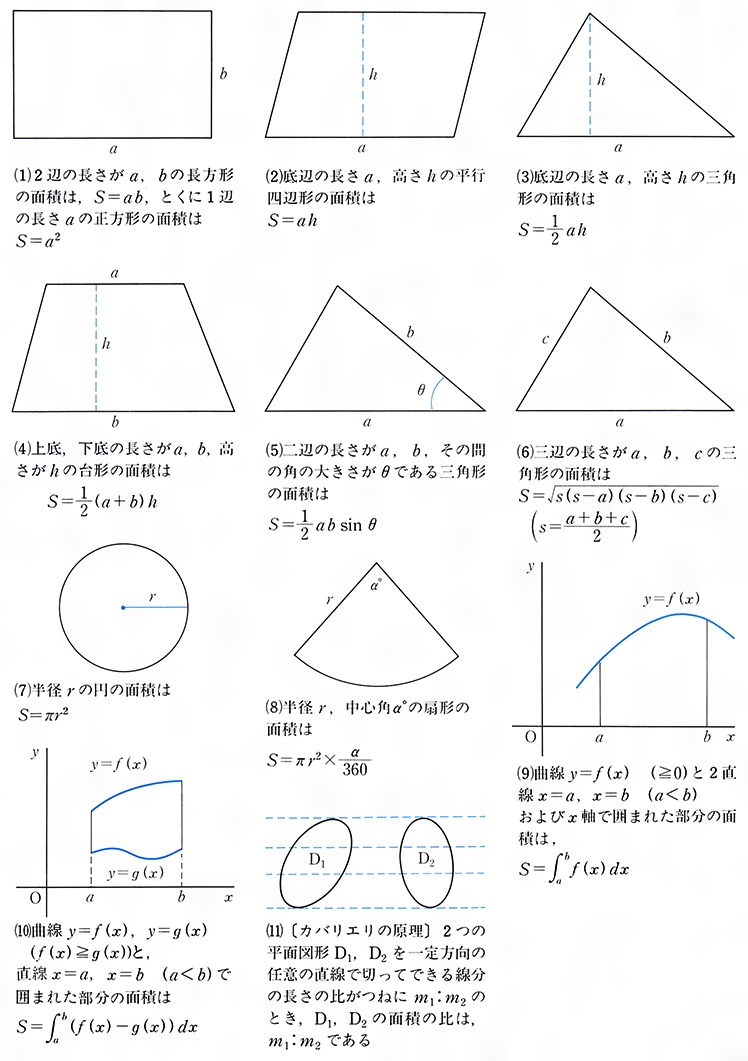



面積とは コトバンク
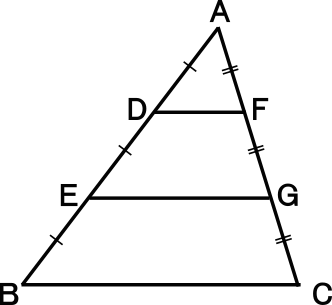



中学3年数学練習問題 相似な平面図形の面積の比 図形と相似



平面図形の面積 復習問題として平面図形のプリントを出され Yahoo 知恵袋




平面図形 ひし形の面積は 一方の対角線 他方の対角線 2 正方形の面積は 対角線 対角線 2 ワンセンテンス算数 Note




つまずきをなくす 小4 5 6 算数 平面図形 Amazon Com Books




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




算数苦手さん向けの 平面図形 円の面積 間違いポイントと対策 新小5 サピックス 中学受験 知識ゼロから合格へ



3



灘中学 08年 平成年度 平面図形の面積 灘中学の算数に挑戦 まいにち一題 中学受験問題研究 灘分校




なぜ 周の長さの比は 25を使うんですか 下の15cmは使わないんですか Clear




中学受験算数 平面図形編 Flashcards Quizlet
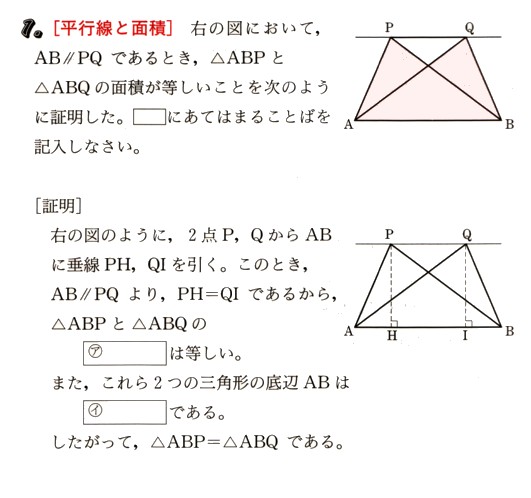



中学2年数学 平面図形 平行線と面積 練習問題1 あんのん塾



平面図形の難問1 日大豊山中




平面図形の苦手を解消 三角形の面積比 基本編
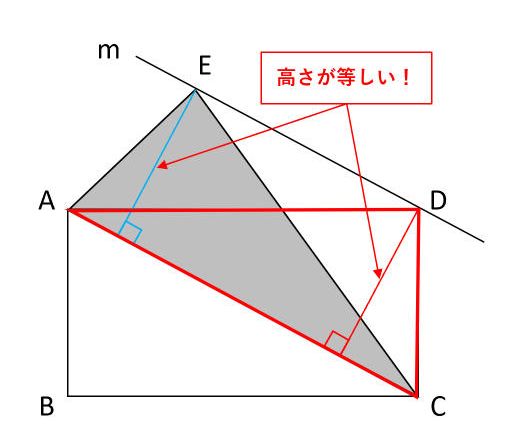



等積変形で難しい面積問題をサクッと解決 平行線と三角形の関係がおもしろい 中学受験ナビ




豊島岡女子中 算数の図形問題 プロが教える重要ポイント




第30回 平面図形 複合図形の求積 5年生 日能研の歩き方




図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト
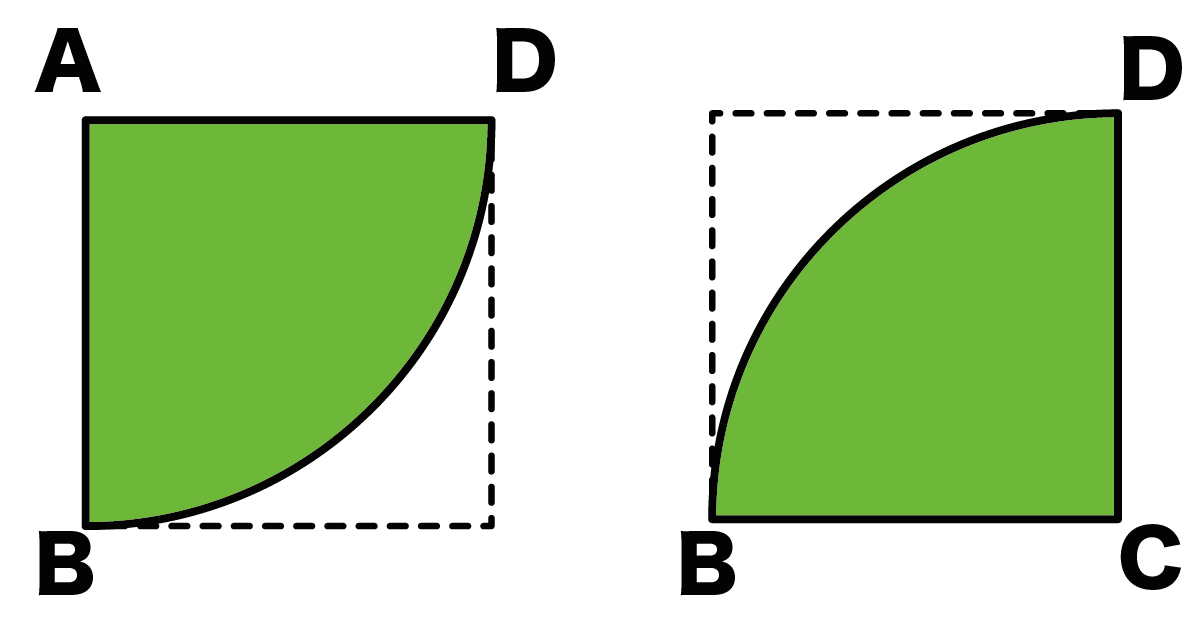



正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿